Triangle Tangled II

Geometry Level 5

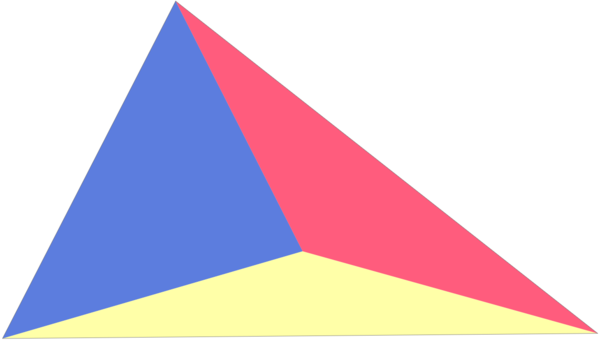
Three triangles of equal perimeters are put together to form a bigger triangle $T$ as shown in the figure.

What is the maximum obtainable value of an angle $\theta$ of triangle $T$ ?

2\tan^{-1}\dfrac{4}{3}

2\tan^{-1}\dfrac{5}{3}

2\tan^{-1}\dfrac{12}{5}

2\tan^{-1}\dfrac{21}{20}

1 solution

Christopher Criscitiello
Feb 2, 2019

Are you sure $2 arctan(4/3)$ is the right answer? I am pretty sure any obtuse triangle cannot be dissected into three triangles (as above) such that each triangle has the same perimeter. However, you can obtain a triangle $T$ whose largest angle is arbitrarily close to (but smaller than) $90$ degrees (consider isosceles triangle whose common angles are near $90$ degrees). I can explain my reasoning further if you want ...

Yes, the answer is correct. I think you should read this article

Digvijay Singh - 2 years, 4 months ago

@Digvijay Singh Thanks for the article! I think the way the article defines the "isoperimetric point" P, P is not required to lie in the interior of the triangle (see Figure 2 from pg. 552); I might be wrong though, I skimmed the paper. I was assuming P has to lie in the interior of ABC. Are you requiring that P lies in the interior of ABC?

Christopher Criscitiello - 2 years, 4 months ago

Triangle Tangled II

1 solution

0 pending reports