Triangle trials
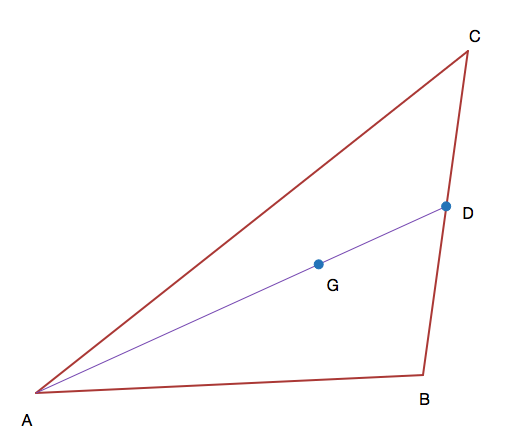 Triangle
A
B
C
with its centroid at
G
has side lengths
A
B
=
1
5
,
B
C
=
1
8
,
A
C
=
2
5
.
D
is the midpoint of
B
C
.
Triangle
A
B
C
with its centroid at
G
has side lengths
A
B
=
1
5
,
B
C
=
1
8
,
A
C
=
2
5
.
D
is the midpoint of
B
C
.
The length of G D can be expressed as b a d , where a and b are coprime positive integers and d is a square-free positive integer.
Find a + b + d + 1 .
The answer is 92.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Done using Appolonius Theorem too :D
Same way except for the fact I used Appolonius theorem to derive the median length :D
Did same but derived the median length formula using Vectors.
its solution is not good enough to understand
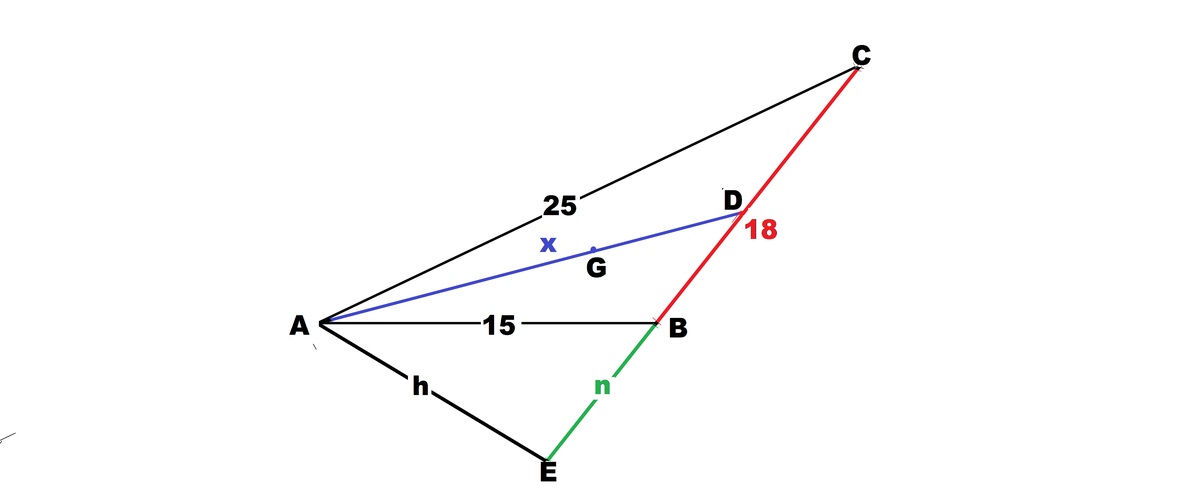
B is an obtuse angle. From A drop perpendicular AE to meet CB extended at E..
Let AE=h , AD=x, BE=n.
h
2
=
1
5
2
−
n
2
a
l
s
o
=
2
5
2
−
(
1
8
+
n
)
2
∴
n
=
9
1
9
.
∴
x
2
=
h
2
+
(
n
+
9
)
2
=
1
5
2
−
n
2
+
(
n
+
9
)
2
⟹
x
2
=
2
2
5
+
1
8
n
+
8
1
=
3
4
4
=
(
2
∗
8
6
)
2
.
G
D
=
x
/
3
=
3
2
∗
8
6
a
+
b
+
d
+
1
=
2
+
3
+
8
6
+
1
=
9
2
9
2
this method is so easy to understand
By Stewart's theorem, man+dad = bmb+cnc, where m = BD, n = DC, a = BC, b = AC, c = AB, and d = AD. So
18 * 9^2+18 * d^2 = 9 * 25^2+9 * 15^2,
d = 2 * sqrt(86).
Therefore GD = d/3 = 2 * sqrt(86)/3. Hence the answer is 2+3+86+1 = 92.
Use Appolonius theorem,find the median 2 * sqrt 86,then 1/3 of it is (2 * 86)/3,so 2+3+86+1=92
Carnot Theorem applied to angle(A) = angle(CAB), leads to:
cos(A) = (|AB|^2 + |AC|^2 - |BC|^2)/(2|AB||AC|);
cos(A) = (15^2 + 25^2 - 18^2)/(2 15 25) = 263/375;
if we denote C1 the projection on axis x of a system of coordinates
(O,x,y),
O := A, x // AB, y ⊥ x in A,
|CC1| = |AC|sin(A) = 25√(1 - (263/375)^2) = √(375^2 - 263^2)/15;
the coordinates of point C are:
xc = |AC|cos(A) = 25*263/375 = 263/15;
yc = |CC1| = √(375^2 - 263^2)/15;
the coordinates of the centroid G are:
xg = (xa + xb + xc)/3 = (0 + 15 + 263/15)/3 = 488/45;
yg = (ya + yb + yc)/3 = (0 + 0 + √(375^2 - 263^2)/15)/3 = √(375^2 -
263^2)/45;
the midpoint D between B and C has coordinates:
xd = (xb + xc)/2 = (15 + 263/15)/2 = 488/30;
yd = (yb + yc)/2 = (0 + √(375^2 - 263^2)/15)/2 = √(375^2 - 263^2)/30;
|AD| = √((xd - xa)^2 + (yd - ya)^2);
|AD| = √((488/30)^2 + (375^2 - 263^2)/30^2) = 2√86;
|GD| = |AD|/3 = (2/3)√86 = (a/b)√d;
the question is the value of a + b + d + 1, so:
a + b + d + 1 = 2 + 3 + 86 + 1 = 92
If u put a \( in front of every line and a \ ) (without the space) at the end of each line it will look much nicer. Eg x+3*2= x + 3 ∗ 2
The coordinates of centroid G are given by:
x G = 3 x A + x B + x C , y G = 3 y A + y B + y C
Let B ( 0 , 0 ) , then C ( 1 8 , 0 ) and D ( 9 , 0 ) . We have:
x A 2 + y A 2 = A B 2 = 1 5 2 = 2 2 5 . . . ( 1 )
( 1 8 − x A ) 2 + y A 2 = A C 2 = 2 5 2 = 6 2 5 . . . ( 2 )
( 2 ) − ( 1 ) : 3 4 2 − 3 6 x A = 4 0 0 ⇒ x A = 3 6 − 7 6 = 9 − 1 9
Substitute x A in equation (1):
( 9 − 1 9 ) 2 + y A 2 = 2 2 5 ⇒ y A = 2 2 5 − 8 1 3 6 1 = 9 2 4 4 6 6
Therefore,
x G = 3 9 − 1 9 + 0 + 1 8 y G = 3 9 2 4 4 6 6 + 0 + 0
= 2 7 1 4 3 = 2 7 2 4 4 6 6
The length G D = ( x G − x D ) 2 + ( y G − y D ) 2
= ( 2 7 1 4 3 − 9 ) 2 + ( 2 7 2 4 4 6 6 − 0 ) 2
= ( 2 7 − 1 0 0 ) 2 + ( 2 7 2 4 4 6 6 ) 2
= 2 7 1 1 0 0 0 0 + 1 7 8 6 4
= 2 7 1 2 7 8 6 4 = 2 7 1 8 8 6 = 3 2 8 6
Therefore, a = 2 , b = 3 , c = 1 , d = 8 6 .
⇒ a + b + c + d = 9 2
Ya, stupid me. You mean cosine rule? The answer as follows:
Let A D = b , then G D = 3 1 b . Let ∠ A B C = θ , then we have:
2 5 2 = 1 5 2 + 1 8 2 − 2 ( 1 5 ) ( 1 8 ) cos θ . . . ( 1 )
Similarly,
b 2 = 1 5 2 + 9 2 − 2 ( 1 5 ) ( 9 ) cos θ . . . ( 2 )
2 × ( 2 ) − ( 1 ) : 2 b 2 − 6 2 5 = 2 2 5 − 1 6 2 ⇒ b = 3 4 4 = 2 8 6
Therefore, G D = 3 1 b = 3 2 8 6
⇒ a = 2 , b = 3 , c = 1 and d = 8 6 ; and a + b + c + d = 2 + 3 + 1 + 8 6 = 9 2
Log in to reply
Wow...I am amazed...No, you are not stupid, I am stupid,,,there are so many ways to do this relatively simple problem, you have shown me two ....Alan has shown me one...and I too have one...such an enriching experience! :D
This could have been simplified, if you did not use co-ordinates. Instead you could have used Appolonius
I agree, its a little clumsy to use coordinates
Long method but a nice idea.
We find A D using a formula for the medians derived from Stewart's Theorem:
A D = 2 2 ( A B 2 + A C 2 ) − B C 2
A D = 2 2 ( 1 5 2 + 2 5 2 ) − 1 8 2
A D = 2 1 3 7 6 = 2 8 6
Now, since the medians cut themselves in the centroid in a ratio of 2 : 1 from the vertex to the midpoint, we have:
G D = 3 A D = 3 2 8 6
Hence, a = 2 , b = 3 , d = 8 6 and a + b + d + 1 = 9 2 .