Triangle Triplets
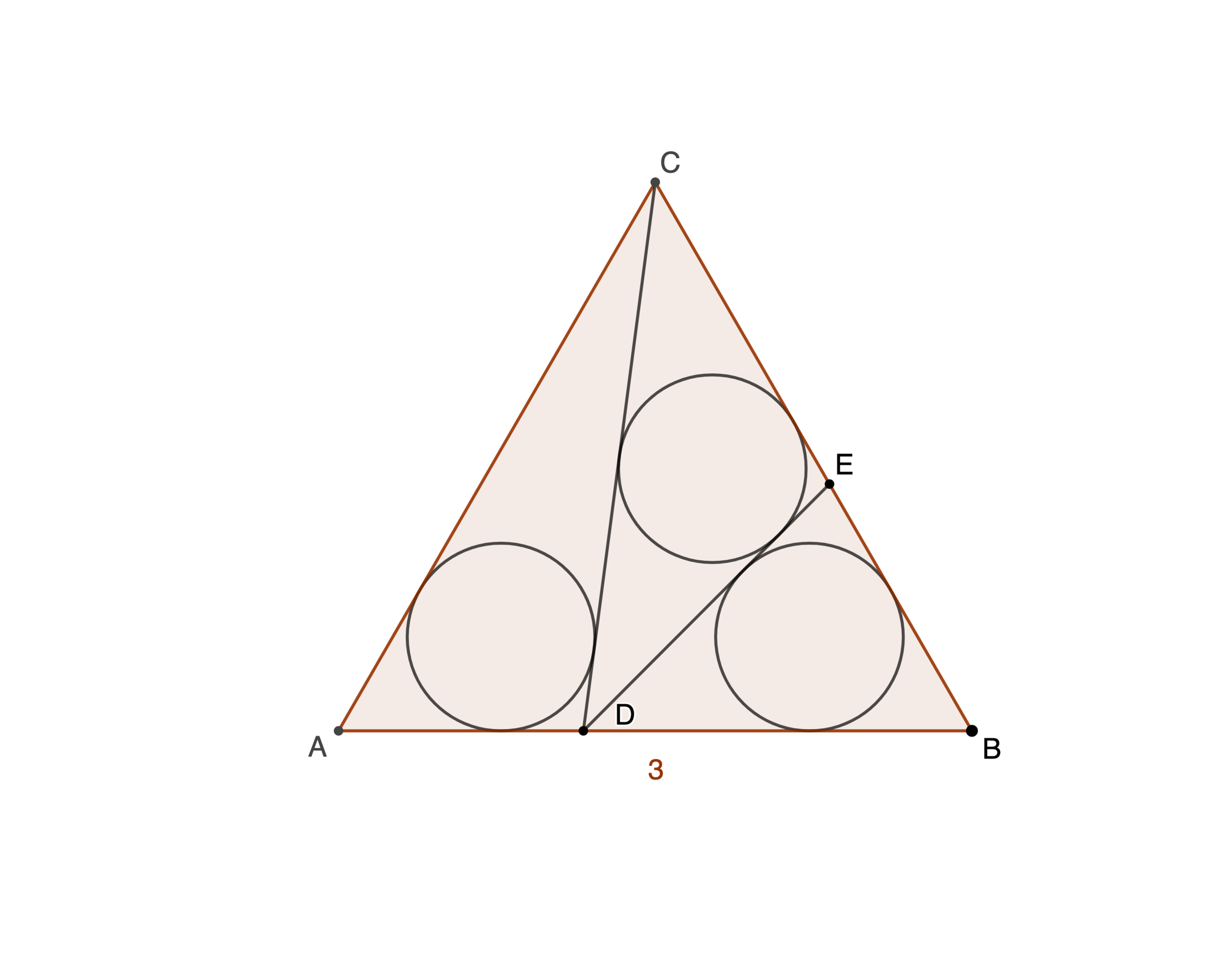
An equilateral △ A B C has a side length 3. D and E are chosen such that the three incircles are congruent. If the length of A D is a root of f ( x ) = a x 3 + b x 2 + c x + d , where g cd ( a , b , c , d ) = 1 and a > 0 , submit f ( 2 ) .
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Nice work! A lot more algebra, than geometry, huh?
Log in to reply
Maybe I substituted the numbers.
f ( x ) = a x 3 + b x 2 + c x + d
f ( 2 ) = 8 a + 4 b + 2 c + d
@Mark Hennings And at the final row, it is not only a real root of f ( x ) .
By the fundamental theorem of algebra , we get 3 roots in the C .(complex number)
Log in to reply
Yes, there are two complex roots, but since x is the length of a line segment, we can assume that we are looking for a real root, and this cubic only has one real root.
0 = 4 x 2 ( ( x 2 + 3 x − 9 ) − ( 3 − x ) x 2 − 3 x + 9 ) ( 3 − x ) ( ( 2 x 2 − 9 ) + ( 2 x − 3 ) x 2 − 3 x + 9 ) ( ( 6 x 4 − 1 2 6 x 3 + 7 2 9 x 2 − 1 5 3 9 x + 9 7 2 ) + 3 ( 3 − 2 x ) ( x 2 + 2 7 x − 3 6 ) x 2 − 3 x + 9 ) If ( 2 x 2 − 9 ) + ( 2 x − 3 ) x 2 − 3 x + 9 = 0 then 0 = ( 2 x 2 − 9 ) 2 − ( x 2 − 3 x + 9 ) ( 2 x − 3 ) 2 = 3 x ( x − 3 ) ( 8 x − 1 5 ) which has no solution with 0 < x < 2 3 . Thus we deduce that ( 6 x 4 − 1 2 6 x 3 + 7 2 9 x 2 − 1 5 3 9 x + 9 7 2 ) + 3 ( 3 − 2 x ) ( x 2 + 2 7 x − 3 6 ) x 2 − 3 x + 9 ( 6 x 4 − 1 2 6 x 3 + 7 2 9 x 2 − 1 5 3 9 x + 9 7 2 ) 2 − 9 ( 3 − 2 x ) 2 ( x 2 + 2 7 x − 3 6 ) 2 ( x 2 − 3 x + 9 ) 8 1 x 2 ( 1 5 − 8 x ) ( 5 x 3 − 9 x 2 + 2 7 x − 2 7 ) = 0 = 0 = 0 and so, since 0 < x < 2 3 , we deduce that f ( x ) = 5 x 3 − 9 x 2 + 2 7 x − 2 7 = 0 which makes the answer f ( 2 ) = 3 1 . Note that the value of x is approximately 1 . 1 5 9 4 6 .