Triangle vs Quad
Geometry
Level
3
The octagon is regular. Which shaded region is larger ?
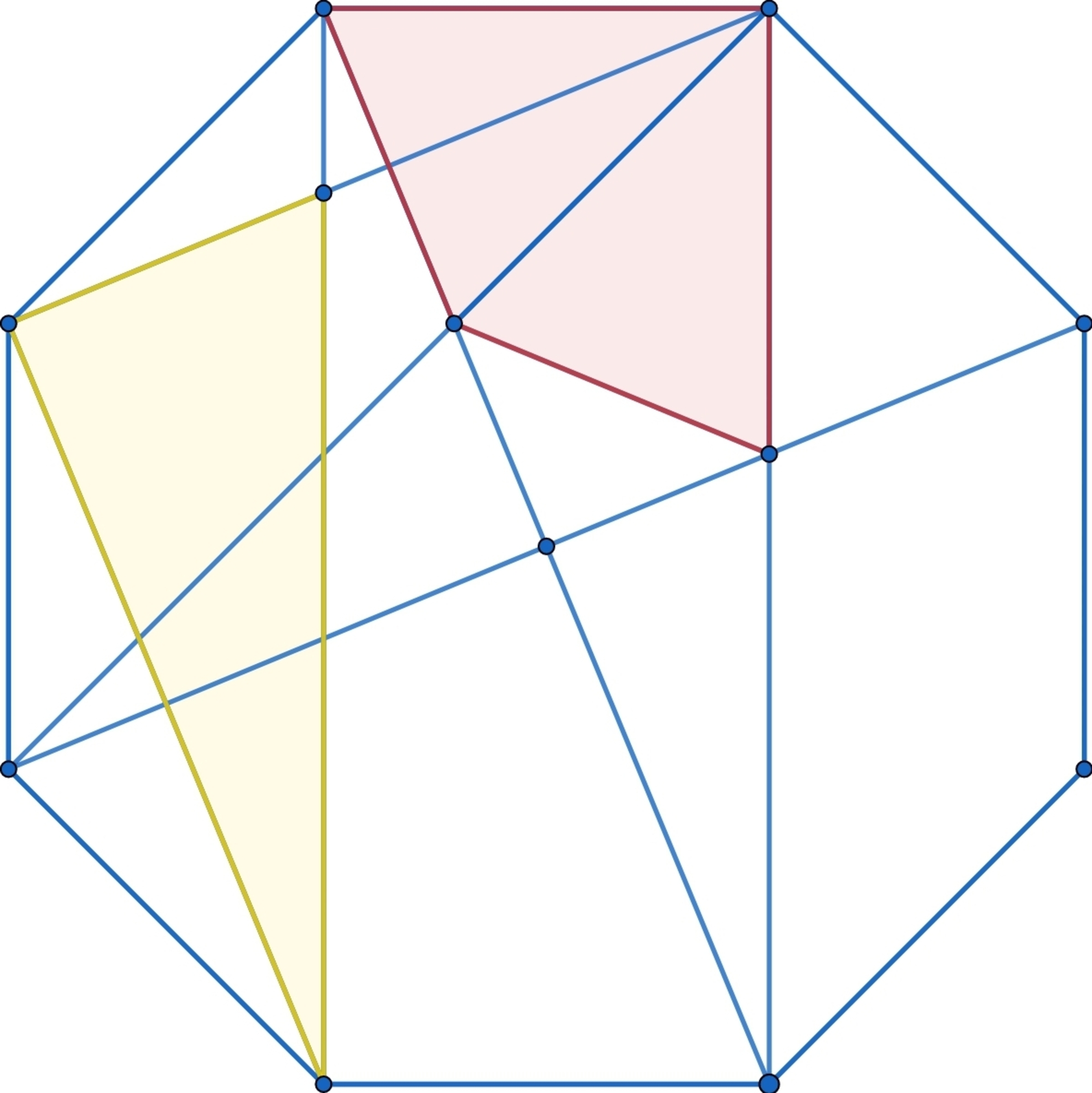
Yellow
Red
Both are equal
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
By simmetry ABC and BCG are congruent to BGE that is congruent o DKI that is congruent to DHI while DIJ has the same area of DKI then
Red Area = Area(ABC) + Area(BCG) = Area(BEFG)=AREA(DIJK)=Area(DIJ) + Area(DJK) = 2 Area(DIK) = Area(DHI) + Area(DIJ) = Yellow Area