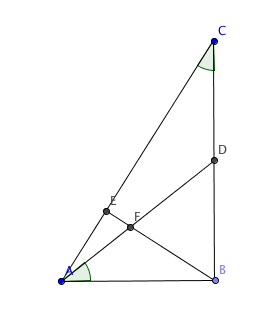
Triangle with an Altitude

Let $\angle BAD = \angle BCA = \theta.$ Then, doing some angle-chasing, we see that $\angle ABF = \theta$ as well, so $AF = BF,$ and that $\angle BFD = \angle BDF = \dfrac{\pi}{2} - \theta,$ so $BF = DF.$ Thus, $AF = BF = DF.$

Now let $BD = DC = x.$ Because $\triangle ABD \sim \triangle CBA,$ we have the equation $\dfrac{AB}{BD} = \dfrac{CB}{AB}$ $\dfrac{36}{x} = \dfrac{2x}{36}$ Solving for $x$ gives $x = 18\sqrt{2}.$ By Pythagoras on right triangle $ABD,$ we have $AD = 18\sqrt{6},$ so $AF = BF = DF = 9\sqrt{6}.$ Also, by Pythagoras on right triangle $ABC,$ we have $AC = 36\sqrt{3}.$

Notice that triangles $ABC$ and $BEC$ are similar, so we have $\dfrac{CB}{EB} = \dfrac{AC}{AB}$ $\dfrac{36\sqrt{2}}{EB} = \dfrac{36\sqrt{3}}{36}$ Solving for $EB$ gives $EB = 12\sqrt{6}.$ Thus, $EF = EB - BF = 12\sqrt{6} - 9 \sqrt{6} = 3\sqrt{6},$ and $EF^2 = \boxed{54}.$

First of all we have to name the angles.

Angles with x value wil be <ACB < DAB <BFA.

Let y denote 90 - x. So <BAC < ADB <FBD have value y.

Since ADB and ACB have the same angles, we can assume they are similar, then so:

$\frac{AB}{DB}$ = $\frac{BC}{BA}$

Since D is the midpoint of BC we get:

$\frac{36}{DB}$ = $\frac{2DB}{36}$

So DB = $\sqrt{648}$

By Pytagoras we get that:

$AB^{2} + DB^{2} = AD^{2}$

So AD = $\sqrt{1944}$

Searching new similar triangles we see that AFB and BFD are isoseles. We also realize that:

AF = FB = FD.

Since AD = AF + FD, we get:

$\sqrt{1944}$ = 2 * AF, and so:

AF = $\frac{\sqrt{1944}}{2}$

So we have the hypotenuse of AEF, and we have to search one the other sides.

Since AEB and ABD are similar we can apply Thales in order to find AE.

$\frac{\sqrt{1944}}{\sqrt{648}} = \frac{36}{AE}$

Hence AE = $\frac{36\sqrt{648}}{\sqrt{1944}}$

And finally we use Pytaoras to find EF

$EF^{2} = AF^{2} - AE^{2}$

$EF^{2} = 486 - 432 = 54$

SOLVED

Let $\angle DAB = \theta \Rightarrow BD = 36 \tan \theta \Rightarrow BC = 72 \tan \theta$ .

From the triangle $ABC$ , $\tan \theta = \frac {36}{72 \tan \theta} \Rightarrow = \frac {1}{\sqrt2}$

Plot the coordinates on the cartesian plane with $A(0,0), B(36,0), C(36,72 \tan \theta )$

Then equation of straight line $AC$ is $y = 2 \tan \theta x = x \sqrt2$

And equation of straight line $AD$ is $y = \tan \theta x = x \frac {1}{\sqrt2}$

$m_{BE} = -\frac {1}{m_{AC}} = -\frac {1}{\sqrt2}$

Equation of $BE$ is $y = -\frac {1}{\sqrt2} (x - 36)$

Comparing straight lines $AC$ and $BE$ , we get $E(12,12\sqrt2)$

Comparing straight lines $AC$ and $BE$ , we get $F(18,9\sqrt2)$

Hence, $EF^2 = (12 - 18)^2 + (12\sqrt2 - 9\sqrt2)^2 = \boxed{54}$

Let $\angle ACB$ = $\angle BAD$ = $\alpha$ and $BC$ = $h$
Of $\Delta$ ABC, $tan$ $\alpha$ = $\frac{AB}{BC}$ = $\frac{36}{h}$
Of $\Delta$ ABD, $tan$ $\alpha$ = $\frac{DB}{AB}$ = $\frac{\frac{h}{2}}{36}$ [ $D$ is the midpoint of $BC$ ]
⇒ $\frac{36}{h}$ = $\frac{\frac{h}{2}}{36}$
⇒ $h^2$ = $2$ . $36^2$
⇒ $h$ = $36$ $\sqrt{2}$
Of right triangle $ABC$ , by Pythagorean Theorem,
$AC$ = $\sqrt{AB^2 + BC^2}$
⇒ $AC$ = $\sqrt{36^2 + h^2}$
⇒ $AC$ = $\sqrt{36^2 + 2.36^2}$
⇒ $AC$ = $36$ $\sqrt{3}$
$\Delta$ $ABC$ and $\Delta$ $ABE$ are similar triangles, so,
$\angle ACB$ = $\angle ABE$
⇒ $\angle BAD$ = $\angle ABE$ [ $\angle ACB$ = $\angle BAD$ , Given ]
So, of $\Delta$ $FAB$ ; $FB$ = $FA$
We know that, $\Delta$ $ABC$ and $\Delta$ $ABE$ are similar triangles, so,
$\frac{AC}{AB}$ = $\frac{AB}{AE}$
⇒ $\frac{36\sqrt{3}}{36}$ = $\frac{36}{AE}$
⇒ $AE$ = $\frac{36}{\sqrt{3}}$
⇒ $AE^2$ = $\frac{36^2}{3}$
Of $\Delta$ $BCE$ , $AD$ is the transversal, so by MENELAUS THEOREM,
$\frac{BD}{DC}$ . $\frac{AC}{AE}$ . $\frac{EF}{FB}$ = $1$
⇒ $\frac{1}{1}$ . $\frac{36\sqrt{3}}{\frac{36}{\sqrt{3}}}$ . $\frac{EF}{FA}$ = $1$ [ $D$ is the midpoint of $BC$ , and $FB$ = $FA$ ]
⇒ $FA$ = $3$ $EF$
OF right triangle $FEA$ , by Pythagorean Theorem,
$FA^2$ = $EF^2$ + $AE^2$
⇒ $(3EF)^2$ = $EF^2$ + $\frac{36^2}{3}$
⇒ $8EF^2$ = $\frac{36^2}{3}$
⇒ $EF^2$ = $54$ [ANSWER]

Let $BD = x \to CD = x$ . We note that $\bigtriangleup ABC \sim \bigtriangleup DBA$ by Angle-Angle similarity. This means that $\frac{AB}{BD} = \frac{BC}{AB} \to \frac{36}{x} = \frac{2x}{36} \to$ $x = 18\sqrt2$ . By the Pythagorean Theorem on $\bigtriangleup ABC$ , $AB^2 + BC^2 = AC^2 \to$ $36^2 + (2\cdot18\sqrt2)^2 = AC^2 \to AC = 36\sqrt3$ .

We now note that $\bigtriangleup ABC \sim \bigtriangleup BEC$ , which means that $\frac{AC}{AB} = \frac{BC}{EB} \to \frac{36\sqrt3}{36} = \frac{36\sqrt2}{EB} \to EB = 36\sqrt\frac{2}{3}$ . Using the Pythagorean Theorem on $\bigtriangleup EBC$ , we have $EC^2 = BC^2 - EB^2 \to$ $EC^2 = 36^2(2-\frac{2}{3}) \to EC = 24\sqrt3$ , and then $AE = 36\sqrt3 - 24\sqrt3 = 12\sqrt3$ . Noting that $EC = 2 \cdot AE$ , we proceed to calculate $EF$ by using Mass Points.

Assign point $B$ a mass of $1$ . Then the mass of $C$ must also be $1$ and the mass of $A$ is $2$ , which means that the mass of $E$ is $3$ . Thus, the ratio $EF:FB = 1:3 \to EF = \frac{1}{4}\cdot EB = \frac{1}{4}\cdot36\sqrt\frac{2}{3} = 9\sqrt\frac{2}{3}$ . We square this value to get the desired value, $EF^2$ , which is $(9\sqrt\frac{2}{3})^2 = 81\cdot\frac{2}{3} = \fbox{54}$ .

given the facts above, we can say that triangles ABC, DAB, BAE, and FAE are congruent with $\theta$ : 36 90 - $\ theta$ : 36 90 : 36 90 : 36 ratios respectively..

through these, it is obvious that it is a 30-60-90 angled triangles..

in the figure above, we are finding the value of F $E^{2}$ of triangle BAE = FAE and as it is written, 90 : 36, which means BA = 36, AE = 18 and EB = 18 $\ sqrt{3}$

thus, FA = 36 AE = 18 and EF = 18 $\ sqrt{3}$

we are finding for the F $E^{2}$ so [18\( \ sqrt{3} ]^{2} ) = 54

From $\angle BAD=\angle BCA$ we get that $\bigtriangleup BCA \sim \bigtriangleup BAD$ . Hence, $\frac{AB}{BD}=\frac{BC}{BA}\rightarrow AB^2=BC*BD$ $\angle CAB=\angle ADB\\\angle BAC=\angle BDA$ Since $D$ is a median, $\displaystyle BC=2BD.$ So $\displaystyle 1296=2BD^2\rightarrow BD=18\sqrt{2} \text{ and } BC=36\sqrt{2}$ . Using $\angle ACB=\angle ECB$ , we get that $\bigtriangleup BCA \sim \bigtriangleup BAD\sim \bigtriangleup ECB$ . Hence, $\angle EBC=\angle BDA\rightarrow FD=FB.$ Now, $\angle BAC+\angle BCA=90^\circ \\\angle EBC+\angle FBA=90^\circ\\\angle BAC+\angle BCA=\angle EBC+\angle FBA\\ \angle BAC+\angle BCA=\angle BDA+\angle FBA\\ \angle BCA=\angle FBA\rightarrow \angle BAD=\angle FBA\rightarrow AF=FB=FD$ Now using the Pythagorean Theorem, we get that $AD^2=DB^2+AB^2=36^2+{18\sqrt{2}}^2=1944\rightarrow AD=\sqrt{1944}\rightarrow FB=\sqrt{486}=9\sqrt{6}$ . In addition, we apply the pythagorean theorem to $\bigtriangleup ABC$ to get $AC^2=AB^2+BC^2=3888\rightarrow AC=36\sqrt{3}$ Let $x=AE$ , now using the geometric mean of $EC$ and $AE$ , we get: $x(36\sqrt{3})=36^2\rightarrow x=AE=12\sqrt{3}$ Finally we apply the pythagorean theorem to $\bigtriangleup AEB$ and $\bigtriangleup ABD$ and get: $AE^2+EB^2=AB^2\\ (12\sqrt{3})^2+(FE+FB)^2=AB^2\\ FE^2+2FE*FB+FB^2=864$ and $AD^2=AB^2+DB^2\\ (AF+FD)^2=1944 \\ AF^2+2AF*FD+FD^2=1944$ Subtracting these two equations gives us. $AF^2-FE^2+2FD(AF-EF)=1080$ . Now, $AF^2-FE^2=432$ and $FD=AF=9\sqrt{6}$ . Substituting these two values in we get: $-18\sqrt{6}FE=-324\\FE=\frac{18}{\sqrt{6}}=3\sqrt{6}$ . So $FE^2=54$

You use a ruler and a protractor :D jk. First, you mark ∠ABE=∠BAD=∠ACB because ΔAEB~ΔBEC~ΔDBA~ΔABC. Using proportions, AB/BC=BD/AB. Since BD=CD, replace the proportion with 36/2(BD)=BD/36. Using cross multiplication, BD=18√2 and BC=36√2.Using pythag, AC=36√3. Using proportions again, AB/AC=AE/AB so 36/36√3=AE/36 and AE=12√3. Using pythag again, EB=12√6. Since ΔAFB is isosceles, AF=BF. Call EF x and BF 12√6-x. Replace BF with AF and use pythag. You end up with x=3√6 so EF^2=54

Using AA similarity, triangle CAB is similar to triangle ADB, so AB/CB = DB/AB meaning that (AB)^2 = (CB)(DB). We know that AB = 36, and since D is the midpoint of CB, CB = 2DB. Thus, we have 36^2 = 2(DB)^2, so DB = 18sqrt(2).

We use Pythagorean to find that AC = 36sqrt(2). And since [ABC] = (AB)(BC)/2 = 36 * 36sqrt(2)/2 = (AC)(BE)/2 = (BE) * 36sqrt(3)/2, we know that BE = 12sqrt(6). Applying Pythagorean on triangle ABE, we find that AE = 12sqrt(3), and since AE + EC = 36sqrt(3), EC = 24sqrt(3).

The ratios of AE:EC = 1:2 and BD:DC = 1:1. Using mass points, we assign A a mass of 2, B a mass of 1, and C a mass of 1. Mass E = Mass A + Mass C = 2 + 1 = 3. Mass F = Mass B + Mass E = 1+3 = 4. From this, we see that the ratio FE:BE = 1:4.

Hence, FE = (BE)/4 = (12sqrt(6))/4 = 3sqrt(6), so (FE)^2 = 54.

Let $A = \{0,0\}$ and $B = \{36,9\}$ .

ADB and CAB are similar triangles as all angles are similar. Hence,

$\frac{36}{2|\text{BD}|}=\frac{|\text{BD}|}{36}\\|\text{BD}|=18 \sqrt{2}\\D=\left\{36,18 \sqrt{2}\right\}$

Since $\angle ABC=90{}^{\circ}$ , $C=\{36,36 \sqrt{2}\}$ .

E is the foot of the perpendicular from B to AC. It must lie on AC.

$E= \lambda \{36,36 \sqrt{2}\}\\E \cdot \{36,36 \sqrt{2}\}=0\\E=\left\{12,12 \sqrt{2}\right\}$

F must lie on both AE and BE.

$F=\lambda_2 \left\{36,18 \sqrt{2}\right\} = \{36,0\} + \mu \left\{12-36,12 \sqrt{2}\right\}\\F=\left\{18,9 \sqrt{2}\right\}$

Hence,

$|\text{FE}|=\sqrt{(18-12)^2+\left(9 \sqrt{2}-12 \sqrt{2}\right)^2}=3 \sqrt{6}\\\left|\text{FE}|^2\right.=54$

Let ∠BAD=∠BCA = alpha

Since tan (alpha) = BD/ AB = AB /BC

then 1/2 BC^2 = AB^2

==> BC =AB*sqrt(2)

tan (alpha) =1/ sqrt(2) ==> alpha = 35.26 degrees

AC^2 = 36^2 + 36^2 (2) ==> AC = 36*sqrt(3)

AE . AC =AB^2 ==> AE =12 sqrt(3)

Use the triangle AEF to solve for FE

with angle FAE = beta

beta can be deduced from 2alpha +beta = 90 deg

Finally FE = 7.348...

and FE^2 = 54

We are given that angle $\angle BAD \cong \angle ACB$ . Therefore we should look for similar triangles. Right off the bat, we see that $\bigtriangleup ABD \cong \bigtriangleup CBA$ . This means that $\frac{AB}{BD}=\frac{CB}{AB}$ . We know that $AB=36$ , and $BD=\frac{CB}{2}$ . Solving, we get $CD=BD=18\sqrt{2}$ and $CB=36\sqrt{2}$ . Using the Pythagorean Theorem, we can find the hypotenuse, which is $AC=36\sqrt{3}$ . We can find $EB$ using area: $\frac{1}{2}AC*EB=\frac{1}{2}AB*BC$ . Solving for $EB$ , we get $EB=12\sqrt{6}$ .

We can then solve for $AE$ and $EC$ . Applying the Pythagorean Theorem again with sides $AE,EB,AB$ , we get $AE=12\sqrt{3} \Longrightarrow EC=24\sqrt{3}$ .

Draw the perpendicular from point $D$ to side $AC$ and call it $I$ . We notice that $\bigtriangleup CID~ \bigtriangleup CEB$ . We can also see that D is the midpoint, to the ratio of the sides is $1/2$ . Therefore, $ID=6\sqrt{6}$ . Apply the Pythagorean Theorem again to $\bigtriangleup CID$ to get $IC$ . $IC=12\sqrt{3}$ . This implies that $AE=EI=IC$ , which means the ratio of the sides of $AEF$ to $AED$ is $1/2$ . Therefore, $FE=3\sqrt{6} \Longrightarrow FE^2=\boxed{54}$ .

Let $BC = a$ . Then, $BD = CD = \dfrac {a}{2}$ . First, notice, from AA similarity, that $\triangle BAD \sim \triangle BCA$ . From this, we can deduce the following: $\dfrac {BA}{BD} = \dfrac {BC}{BA} \implies \dfrac {36}{\dfrac {a}{2}} = \dfrac {a}{36} \implies a = 36\sqrt{2}.$ Now, we use a coordinate system. Note that this is different than that depicted in the problem diagram. The problem can be done in a similar manner using an equally effective coordinate system.

Let $C$ be the point $(0, 0)$ . Let $B$ be the point $36 \sqrt {2}, 0$ . It follows that $A$ is the point $36\sqrt{2}, 36)$ , and $D$ is the point $(18\sqrt{2}, 0)$ .

This gives us that the equation of line $\overline {DA}$ is $y = \sqrt {2}x - 36$ and the equation of line $\overline {EB}$ is $y = -\sqrt{2} x + 72$ .

Note that $F$ is the intersection of these two lines. We find its coordinates. $\begin{aligned} -\sqrt{2}x+72 &=& \sqrt{2}x-36 \\ 2\sqrt{2}x &=& 108 \\ \sqrt{2}x &=& 54 \\ x &=& 27\sqrt{2}. \end{aligned}$ Thus, $F$ is the point $(27\sqrt{2}, 18)$ . Finally, we need to find $FE$ . To do this, note that $FE = EB - FB$ and that $\overline{EB}$ is an altitude. So we can find it. We have equality of areas: $\dfrac {EB \cdot AC}{2} = \dfrac {AB \cdot BC}{2} \implies 36 \cdot 36 \sqrt {2} = EB \cdot 36 \sqrt{3}.$ Solving for $EB$ , we get $\dfrac {36}{\sqrt{6}} = 6\sqrt{6}$ . Finally, we use the Distance Formula to find $FB$ and we get $9 \sqrt{6}$ .

We obtain $|EB| = 3\sqrt{6}$ . A negative length may result due to the inversion of a coordinate system, but our answer is perfectly symmetric otherwise. We get $FE = 3\sqrt{6},$ so $FE^2 = \boxed {54}$ .

From similarity between triangles ABD and CBA results BC=36 $\sqrt{2}$ , next AC=36 $\sqrt{3}$ and BE=12 $\sqrt{6}$ . The triangle FBD is isosceles, let G belong [BD] so that FG is height (altitude) and median. But, if G is the middle of [BD], F will be the middle [AD] (FG and AB are parallel lines, Reciprocal Theorem) and FG=18. In triangle FGB, FB=9 $\sqrt{6}$ that implies EF=3 $\sqrt{6}$ . Finally, EF $^{2}$ =54 :)

Let BD = CD = a and Angle BCA=Angle BAD = C

Given that AB = 36

Now since Triangle ABC and DBA are similar triangles

Therefore, AB/BD=BC/AB

Here AB = 36, BC = 2a and BD = a

Therefore, BC = 36√2

Tan C = 36/(36√2)= 1/√2

Sin C = 1/√3, Cos C = √2/√3

From triangle ABC and ABE, angle ABE = C, angle FAE = 90 -2C

Therefore AE = 36 Sin C

From triangle FAE, FE = (18 Cos 2C)/(Cos C) = 3√6

Hence, FE^2 = 54

As the hypothesis, $∠BAD = ∠BCA$ and $\angle ABC = 90^\circ$ . Thus:

$\tan ∠BAD = \tan ∠BCA$

$\Leftrightarrow \frac {BD}{AB} = \frac {AB}{BC}$

$D$ is the midpoint of $BC$ , this implies that $BC = 2BD$ . Thus:

$BC = 2BD = AB\sqrt 2$

We have $∠BEA = ∠ABC = 90^\circ$ , thus $∠EAB = ∠ACB = ∠BAD$ and $\Delta AFB$ is an isosceles triangle with $AF = BF$ . In addition, $∠ABD$ is a right angle, thus $F$ is the midpoint of $AD$ ( $F$ is the center of the circle which pass $A$ , $B$ , $D$ ), this implies:

$BF = AF = \frac {AD}{2} = \frac {\sqrt{AB^2 + BD^2}}{2} = \frac {\sqrt 6}{4}AB$

We also have:

$\sin ∠BAC = \frac {BC}{AC} = \frac {BE}{AB}$

$\Leftrightarrow BE = \frac {AB \cdot BC}{AC} = \frac {AB \cdot BC}{\sqrt {AB^2 + BC^2}} = \frac {\sqrt 6}{3}AB$

Therefore, $EF = BE - BF = \frac {\sqrt 6}{12}AB = 3\sqrt 6$ . And the final solution of the problem is $EF^2 = 54$ .

It is easy to see that $ABC$ is similar to $AEB$ . $\angle AEB = 90^{\circ}$ and $\angle BCA = \angle BCA$ . Since $D$ is the midpoint of $BC$ , we have: $\frac{BD}{AB} = \frac{AB}{2BD}$ .

Plugging in 36 for $AB$ , we can solve the ratio: $BD = 18\sqrt{2}$ .

Since $ABC$ is similar to $AEB$ , $\angle ABE = \angle C \therefore \angle ABE = \angle BAD$

$\therefore ABF$ is isosceles

Draw a perpendicular from $F$ to $AB$ . Call the intersection of the perpendiculars $G$ . Since $ABF$ is isosceles, $FG$ also bisects $AB$ , thus $AG = BG = 18$ . Also, $AGF$ is similar to $ABD \therefore BF = AF = \frac{1}{2}AD$ .

$AD = \sqrt{AB^2 + BD^2} = 18\sqrt{6} \therefore BF = 9\sqrt{6}$

$AEB$ can be easily shown to be similar to $DBA$ . Thus, we have the ratio $\frac{AB}{AD} = \frac{EB}{AB}$ , which we can solve to find $EB = 12\sqrt{6}$ .

$EF = EB - BF = 12\sqrt{6} - 9\sqrt{6} = 3\sqrt{6}$ $\therefore EF^2 = 54$

We have $\Delta$ $ABD$ and $\Delta$ $CBA$ are similar triangles, so $AB^2$ = $BD.BC$ = $\frac{1}{2}.BC^2$

--> $AB^2$ = $\frac{1}{2}BC^2$ <=> $BC = AB\sqrt{2}$ --> $AC = AB\sqrt{3}$

We also have $\Delta$ $AEB$ similar with $\Delta$ $ABC$ => $AB^2$ = $AE.AC$

--> $AE^2 = \frac{1}{3}AB^2$

Then let $\alpha$ , $\beta$ and $\theta$ be angle $BAD$ , $BAC$ and $FAE$ respectively, from trigonometry we get $tan \theta = \frac{\tan \beta - \tan \alpha}{1 + \tan \beta.\tan \alpha}$ = $\frac{\sqrt{2} - \frac{\sqrt{2}}{2}}{2} = \frac{\sqrt{2}}{4}$

For $\Delta$ $AEF$ is a right triangle so $FE^2 = AE^2\tan^2 {\theta} = \frac{1}{3}AB^2\frac{1}{8} = 54$

let, $\angle ACB = \angle DAB = x$ . For $\bigtriangleup ABC$ and $\bigtriangleup ABD$ ,

$tan(x) = \frac{AB}{BC} = \frac{BD}{AB}$

As , $BD = \frac{1}{2} BC$ , $tan(x) = \frac{1}{\sqrt{2}}$

for $\bigtriangleup ABE$ , as $\angle BAE = 90^\circ - x$ , $\angle ABE = x$

Hence , $\angle EFA = 2x$ , $\angle EAF = 90^\circ - 2x$

Using sine rule in $\bigtriangleup AEF$ ,

$\frac{EF}{cos(2x)} = \frac{AE}{sin(2x)}$

$EF = cot(2x) AE$

$AE = \frac{1}{\sqrt{3}} AB$

Also , $tan(2x) = 2(1/\sqrt{2})/(1-(1/2)) = 2\sqrt{2}$

Hence , $AE^2 = \frac{36*36}{8*3} = 54$

In triangles ADB and CAB,

Angle DAB = Angle ACB (Given)

Angle ABD = Angle CBA = 90 degree (Common angle)

So, triangles ADB and CAB are similar. (AA Similarity)

So, we have $\frac{AB}{CB}$ = $\frac{DB}{AB}$ which is equivalent to $AB^{2}$ = $CB \times DB$

which is also equivalent to $AB^{2}$ = $\frac{1}{2}$ $CB^{2}$

Through simple calculation, one will get CB = 36 $\sqrt{2}$

By Pythagoras theorem, AC = 36 $\sqrt{3}$ and AD = 18 $\sqrt{6}$

Now observe that triangle CEB is a right angled triangle with angle CEB as 90 degree. This means that a circle with diameter CB can pass through the vertices of this triangle. AB will hence be the tangent to this circle at B.

So, by the Tangent Secant theorem, we have $AB^{2}$ = $AE \times AC$ .

This means that AE = 12 $\sqrt{3}$

Now observe triangle AFB. From the earlier part, we have arrived at the conclusion that AB is the tangent to the circle with diameter CB. So by Tangent chord theorem, we have angle FBA = angle ECB = angle FAB. This means that triangle AFB is isosceles with AF = FB.

Now observe triangle FDB. We have angle FBD = 90 - angle FBA and angle ADB = 90 - angle FAB too. This means that triangle FDB is isosceles with FB = FD.

However, since we have shown that AF = FB, then AF = FD.

This will mean that AF = 9 $\sqrt{6}$

Hence, by applying Pythagoras theorem again, one will get $FE^{2}$ = 54

Since $\angle$ $BAD$ = $\angle$ $BCA$ $\implies$ $\angle$ $BDA$ = $\angle$ $BAC$ $\big($ Using angle sum property in triangles ABD and ABC $\big)$ and $\angle$ $ABD$ = $\angle$ $CBA$ = $90^{\circ}$ $\implies$ $\bigtriangleup$ $ABD$ $\sim$ $\bigtriangleup$ $CBA$ .

$\implies$ $\frac{AB}{BD}$ = $\frac{CB}{BA}$

$\implies$ $BD$ = $18$ $\sqrt2$

Using Pythagorean theorem in $\bigtriangleup$ $ABC$ we find $AC$ = $36$ $\sqrt3$ , and for a right angled triangle we obviously have $AB$ $\times$ $BC$ = $AC$ $\times$ $EB$ $\implies$ $EB$ = $36$ $\sqrt{\frac{2}{3}}$ .

Again using Pythagorean theorem in $\bigtriangleup$ $AEB$ we find $AE$ = $\frac{36}{\sqrt3}$ .

Now $\angle$ $BDA$ = $\angle$ $BAC$

$\implies$ $\tan$ $\angle$ $BDA$ = $\tan$ $\angle$ $BAC$

$\implies$ $\frac{AB}{BD}$ = $\tan$ $($ $\angle$ $BAD +$ $\angle$ $FAE$ $)$

$\implies$ $\sqrt2$ = $\frac{\frac{FE\sqrt3}{36} + \frac{1}{\sqrt2}}{1-\frac{FE\sqrt3}{36\sqrt2}}$

Simplifying out gives $FE$ = $\frac{18}{\sqrt6}$ . So $FE^{2}$ = $\boxed{54}$

First, we determine angles. Let $\angle DAB=\alpha$ , then $\angle ADB=\pi/2-\alpha$ , $\angle ADC=\pi/2+\alpha$ , $\angle DAC=\pi/2-2\alpha$ , and $\angle EBA=\alpha$ . Hence the triangles $AFB$ and $BFD$ are both isosceles, with $AF=BF=FD$ .

The rest can now be computed analytically. Let $B=(0,0)$ , $A=(36,0)$ , and $C=(0,x)$ . Then $D=(0,x/2)$ , and as $F$ is the midpoint of $AD$ , we have $F=(18,x/4)$ . As $\overrightarrow{BF}\perp \overrightarrow{AC}$ , their dot product must be zero, which gives $x=36\sqrt{2}$ . Let $E=A+p\cdot \overrightarrow{AC}=q\cdot \overrightarrow{BF}$ . This solves to $p=1/3$ , $q=4/3$ . Thus, $\overrightarrow{EF}=(q-1)\cdot \overrightarrow{BF}=(1/3)\cdot (18,9\sqrt{2}) = (6,3\sqrt{2})$ and therefore $EF^2 = 6^2 + (3\sqrt{2})^2 = 36 + 18 = \fbox{54}$ .