Triangle within Hexagon
Geometry
Level
2
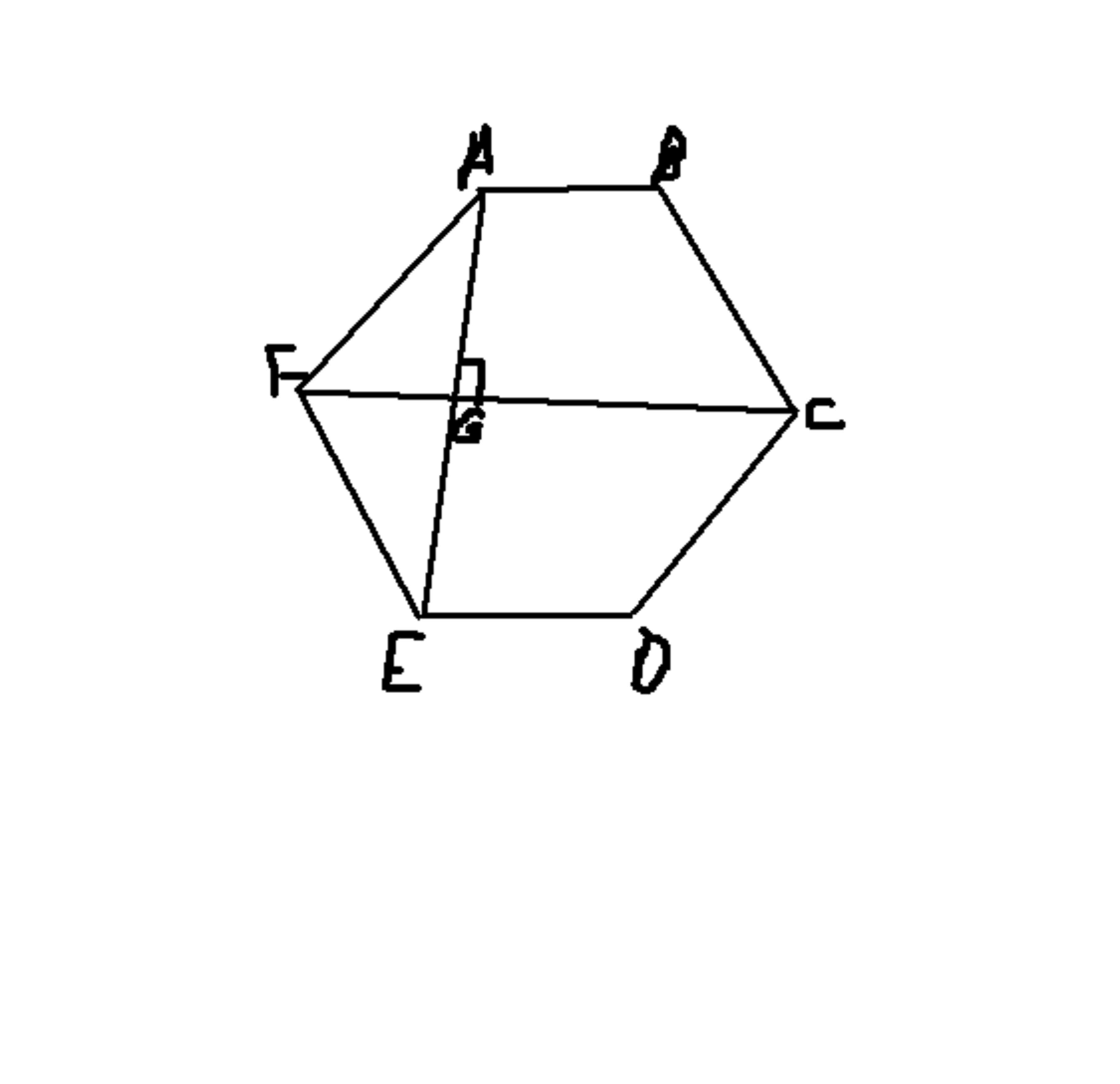
Figure ABCDEF is a regular hexagon. Line FC bisects angle AFE. If the length of ED is12, what is the length of FG?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Using the interior angle sum theorem, (n-2) 180 we could determine the interior angles of the regular polygon as 720 degrees. Dividing it by 6 to get the measurement of one interior angle, we get 120 degrees. It was said that line FC is an angle bisector, therefore, angles AFG and EFG are both equal to 60 degrees. Now since it was a regular polygon, it means that it has equal sides so we take 12 units as the length of every side. Forming a 30-60-90 triangle, it appears that segments FG=side a, GA=side b and FA=side c. Since side a=(side c/2) as stated in the law of special 30-60-90 triangles and we have 12 units for side c, therefore, side a is equal to 6. Hence, segment FG is equal to 6.