Triangleception Part II
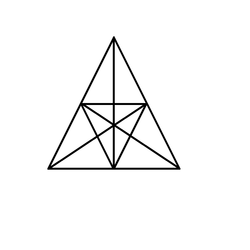Count the number of Triangles in this figure:
This problem is a part of the set Triangleception
The answer is 47.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
There are a total of 9 lines.
Total number of triangles that could be made with 9 lines = ( 3 9 )
However, since there are parallel lines and few lines intersect at a point, hence some combinations don't produce any triangle.
There are three pairs of parallel line, e..g base of the outer and inverted inner isosceles triangle.
Extra triangles counted because of 3 pairs of parallel line = 3 × 7 = 2 1
Three lines intersect at the corners of the outermost isosceles triangle and at the center-most point.
Four lines intersect at the each corner of the innermost isosceles triangle.
Extra triangles counted because of lines intersecting at point = 3 + 1 + 4 × 3 = 1 6
Since none of the lines intersect outside the outermost triangle, hence all the triangles by these 9 lines can be formed only inside outermost triangle.
Total number of effective triangles = ( 3 9 ) − 2 1 − 1 6 = 4 7 .
I just wrote this script to do process this problem and others like it.
Result in blink of an eye.
Log in to reply
You mean my code isn't self-explanatory? ;)
First, the diagram with intersections numbered, as used in the code.
The LINES list represents the lines in the given triangle as a list of lists. Each list must be in lexicographic order. The numbers of the points are recovered from LIST and stored in the POINTS list.
combinations, from the itertools module, is a Python function that calculates all of the combinations of n objects taken r at a time.
I wanted a code that I might be able to apply to problems beyond this one. For that reason, this one looks for triangles of zero area. I also suspected that this might make the code a little faster.
The triples dictionary accumulates triples of points that lie on the same line. (Triples that form zero-area triangles.)
For each LINE the code accumulates a list in pairs_list of all possible pairs of points from LINE. (These are all possible triangle sides for each LINE.)
Now the code takes all combinations of three points at a time. It ask whether the three are in triples. If not, it looks at each combination of two of the three points to ask whether they form the sides of a triangle.
Log in to reply
Thanks!! This makes things much clearer :)
Yes, all that we needed to do was encode what lines existed (which, arguably I would prefer to simply list all pairs of points that are in a line segment, because I think that is more obvious / easier to check), and then run through all triples of points and see if all 3 pairs of lines exists.
At first don't draw the whole diagram - just draw a large (roughly) isosceles with its medians. Now there are 16 triangles (6 single triangles, 3 double triangles, 6 triple triangles and the whole triangle itself). Adding the middle triangles produces another 16 triangles (similar to the ones counted before). However we have 9 new triangles on the outside along with 6 new slanted triangles (with a median as its hypotenuse).
T h i s p r o d u c e s 1 6 + 1 6 + 9 + 6 = 4 7 t r i a n g l e s
I counted all the triangles and solved the question.
There are 9 cases according to me :
C
a
s
e
1
: All the small fragments :
1
2
C
a
s
e
2
: Two at a time :
6
C
a
s
e
3
: Half at a time =
2
×
3
:
6
C
a
s
e
4
:Half at a time =
2
×
3
:
6
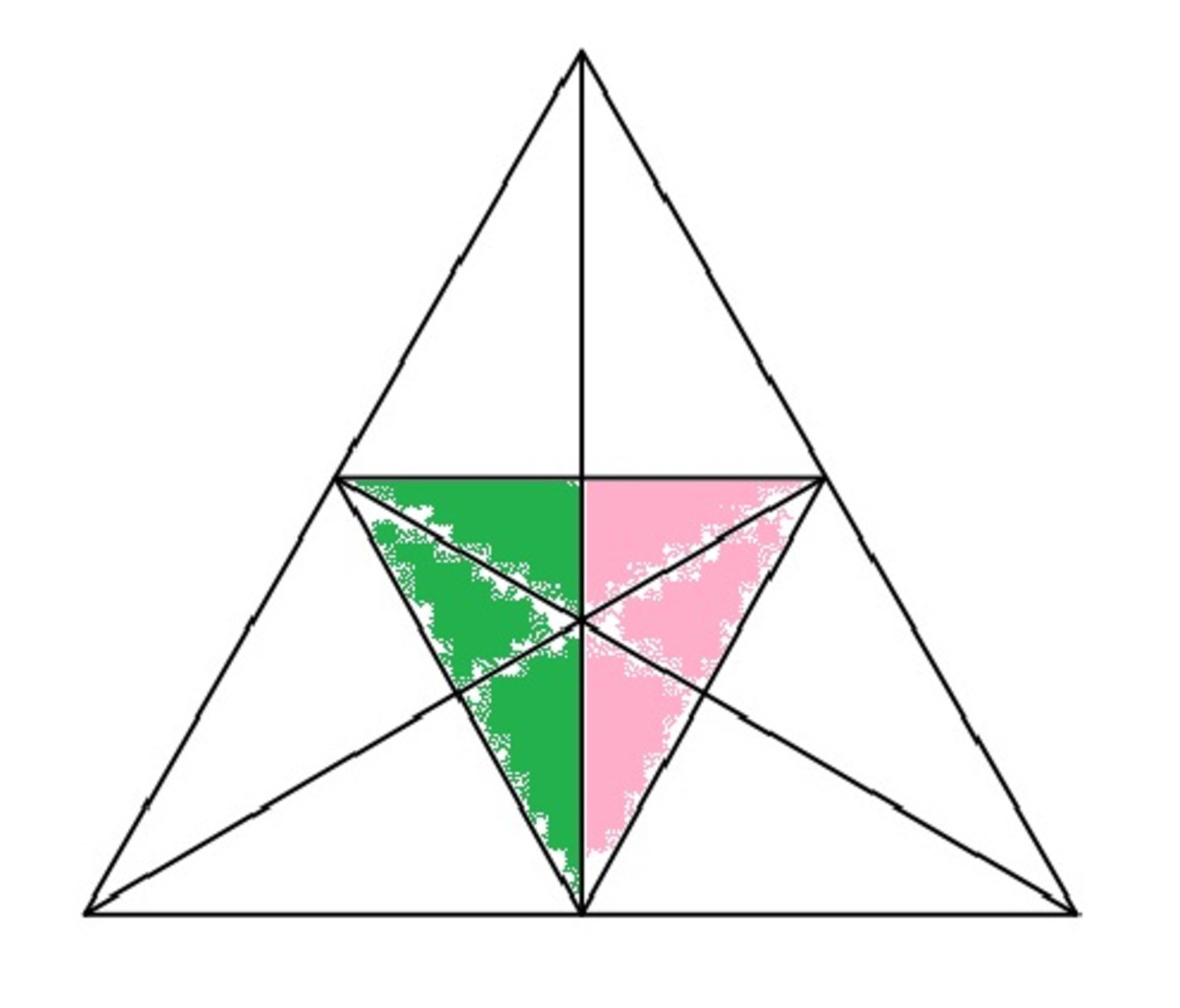
C
a
s
e
5
: One-third a time :
3
C
a
s
e
6
:Half at a time from each vertex =
2
×
3
:
6
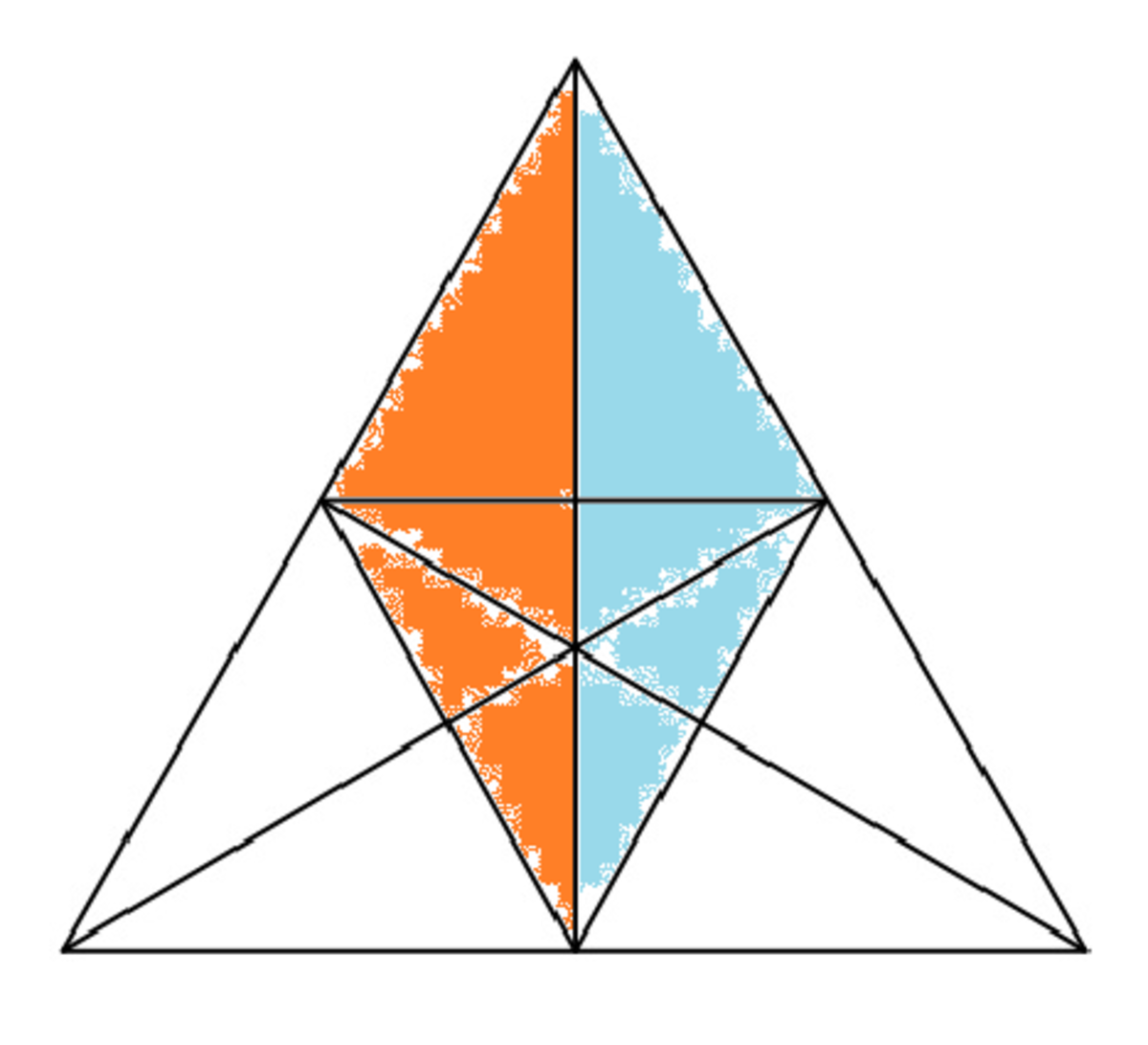
C
a
s
e
7
: Just parts :
6
C
a
s
e
8
: Big triangle as a whole :
1
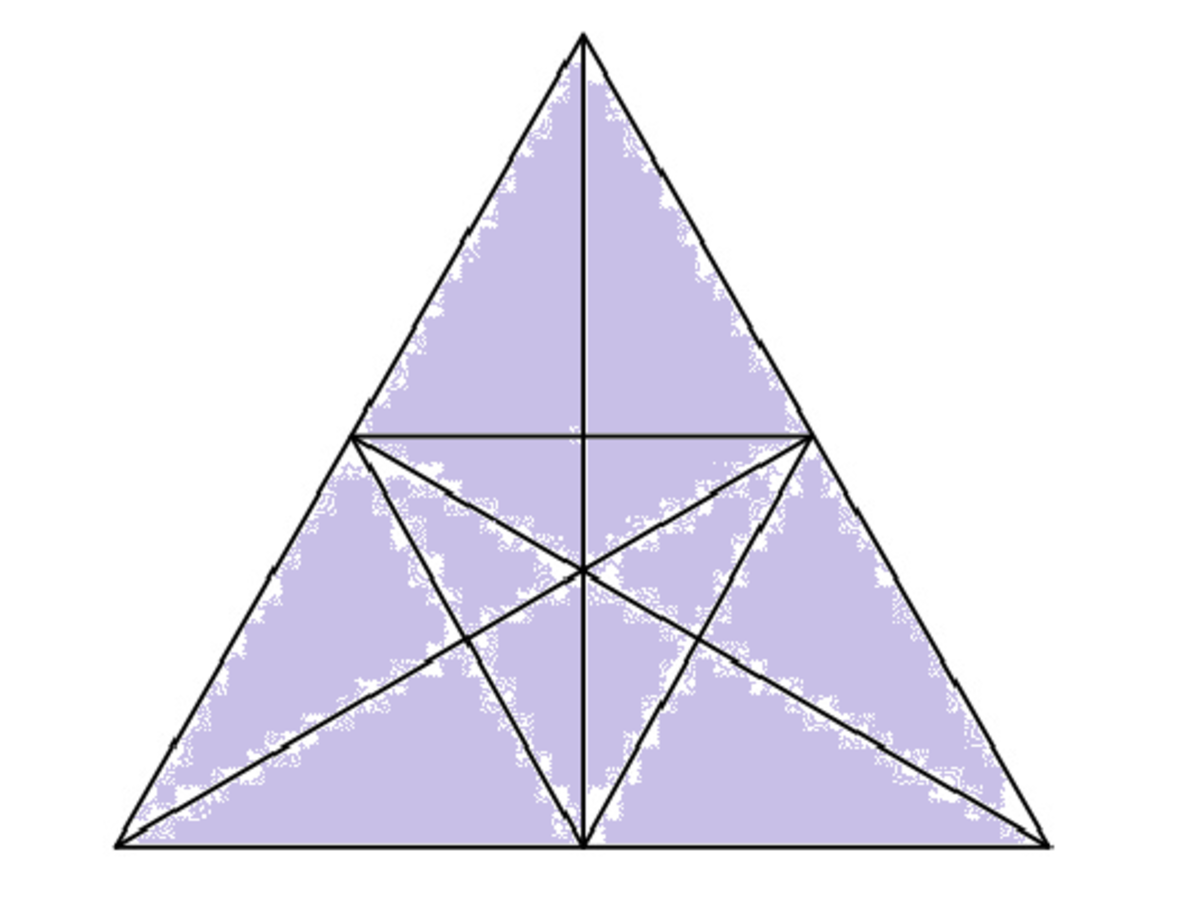
C
a
s
e
9
: Small triangle as a whole :
1
Thus total number of triangles : 4 7
Can you please explain your solution?
Hi Yunhao, can u describe it briefly in words?
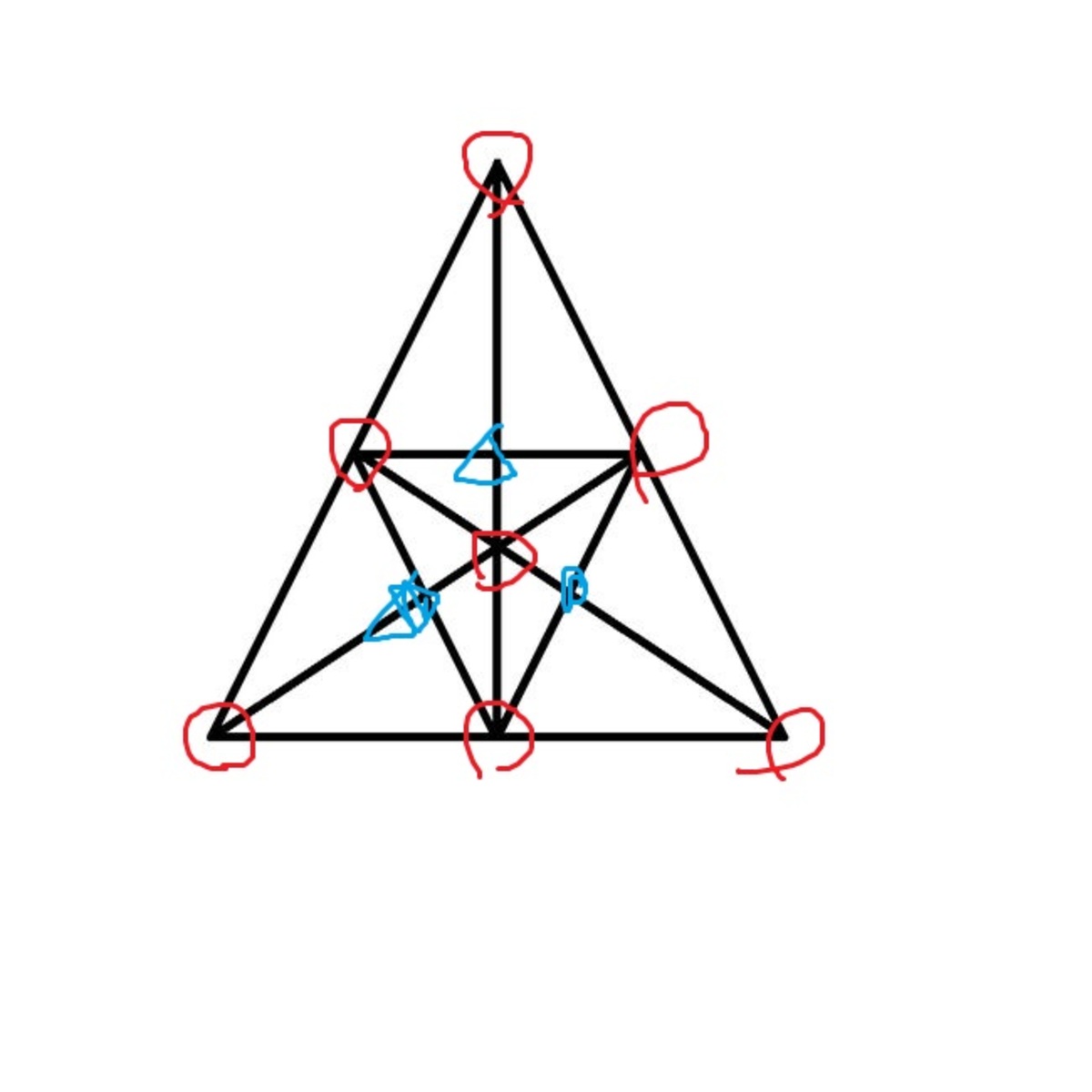
There are 12 triangles with one triangle in it.
There are 12 triangles with two triangles in it
There are 6 triangles with three triangles in it.
There are 9 triangles with four triangles in it.
There are 7 triangles with six triangles in it.
There is 1 triangle with twelve triangles in it.
12+12+6+9+7+1=47.