Median Triangles!

It goes like this

$\frac{3}{4}(a^{2}+b^{2}+c^{2})=m_{a}^{2}+m_{b}^{2}+m_{c}^{2} \qquad (1)$

where $m_{a},m_{b},m_{c}$ are the medians of a triangle

And OA,OB,OC are $\frac{2}{3}$ rd of their respective medians.

$\frac{AB^{2}+BC^{2}+CA^{2}}{OA^{2}+OB^{2}+OC^{2}}=(\frac{9}{4})(\frac{(a^{2}+b^{2}+c^{2})}{(m_{a}^{2}+m_{b}^{2}+m_{c}^{2})})$

from (1)

$\frac{(a^{2}+b^{2}+c^{2})}{(m_{a}^{2}+m_{b}^{2}+m_{c}^{2})}=\frac{4}{3}$

Now,

$\frac{AB^{2}+BC^{2}+CA^{2}}{OA^{2}+OB^{2}+OC^{2}}=\frac{4*9}{3*4}=\boxed3$

As the question is stated the ratio is constant for all triangles . Assume it to be an equilateral triangle . then this is a very easy one . Now to reduce calculation take the side of the triangle to be be $\sqrt{3}$ and then the length of all the medians will be $\frac{3}{2}$ and the centeroid divide the median in the ratio of 2:1 where 1 ia towards the base and so the value of the denominator will be 3 and the numerator will be 9 . $\square$

This is by no means an actual proof, but I wanted to share a nice related construction I know of.

First, notice that the problem is equivalent to $\frac{3}{4}(a^2 + b^2 + c^2) = m_a^2 + m_b^2 + m_c^2$ because $OA = \frac{2}{3}m_a$ , etc.

Now consider:

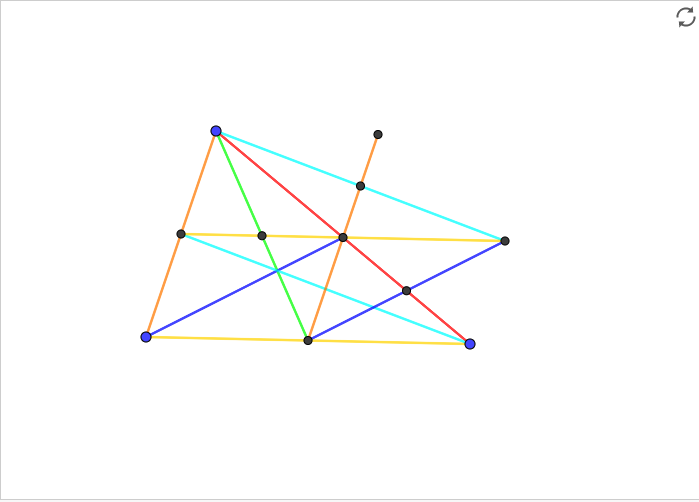
The three blue dots are the vertices of the original triangle. Notice that its medians are the green, cyan, and blue segments. By translating the yellow segment up as shown, we can rearrange the three medians so that they form a triangle.

Now consider the medians of the new triangle. By translating the sides of the original triangle (red, orange, yellow) as shown, we can see that the lengths of the new medians are $\frac{3}{4}$ the lengths of the original sides. Calling the lengths of these new medians $n_a, n_b,$ and $n_c$ , this means $(\frac{3}{4})^2(a^2 + b^2 + c^2) = n_a^2 + n_b^2 + n_c^2$ , which is essentially the problem applied twice.

Nice question! Had so much fun solving it. You can use the Apollonius theorem (special case of Stewart's theorem), but this solution just uses the fact that the centroid of a triangle divides each median in the ratio $2 : 1$ along with some basic trigonometry. In the diagram below, let $AB = A, BC = B$ and $AC = C$ . Also, let $OA = a,OB = b,$ and $OC = c$ . Observe that the centroid is twice as far from each vertex as it is from the point where the median bisects the opposite side. (E.g. $\frac {3}{2}a = AE$ )

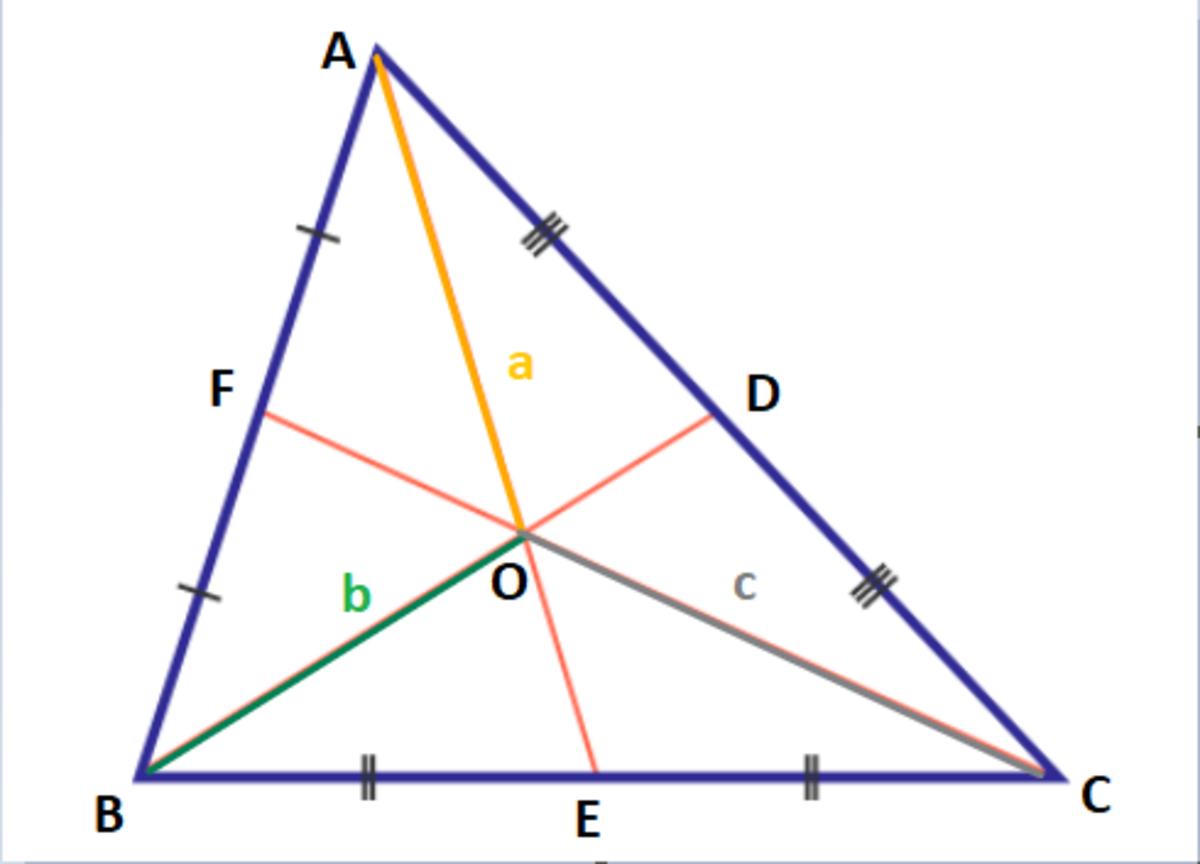
By the law of cosines, we have -

$(\frac {B}{2} )^ {2} + (\frac {3a}{2})^ {2} - 2 \cdot (\frac {B}{2})(\frac {3a}{2}\cos \angle AEC) = C^ {2} . . . . . . . (1) (For \triangle AEC)$

$\Rightarrow \frac {B^ {2}}{4} + \frac {9}{4}a^ {2} - \frac {3aB}{2}\cos \angle AEC = C^ {2} . . . . . . . . . (2)$

Similarly for $\triangle AEB$ , $\frac {B^ {2}}{4} + \frac {9}{4}a^ {2} + \frac {3aB}{2}\cos \angle AEC = A^ {2}$ ( $\because \cos (\pi - x) = -\cos x$ )

Adding $(1)$ and $(2)$ gives us $A^ {2} + C^ {2} = \frac {B^ {2} + 9a^ {2}}{2}$ . Repeating this process for $(\triangle CDB, \triangle ADB)$ and $(\triangle BFC, \triangle AFC)$ gives us -

$\frac {C^ {2} + 9b^ {2}}{2} = A^ {2} + B^ {2}$ and $\frac {A^ {2} + 9c^ {2}}{2} = B^ {2} + C^ {2}$ . Therefore,

$a^{2} = \frac {2A^{2} + 2C^ {2} - B^{2}}{9}$ , $b^{2} = \frac {2A^{2} + 2B^ {2} - C^{2}}{9}$ and $c^{2} = \frac {2B^{2} + 2C^ {2} - A^{2}}{9}$ . So we can conclude that, $\boxed {\frac {A^ {2} + B^ {2} + C^ {2}}{a^ {2} + b^ {2} + c^ {2}} = \frac {A^ {2} + B^ {2} + C^ {2}}{\frac {3(A^ {2} + B^ {2} + C^ {2})}{9}} = 3}$