Triangles and areas
In a triangle , let denote its centroid and let , be points in the interiors of the segments , ,respectively, such that , , are collinear. If denotes the ratio of the area of triangle to the area of and (a and b are co-prime natural numbers.). Find the value of
NOTE:- This question was asked in KVPY -2013
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
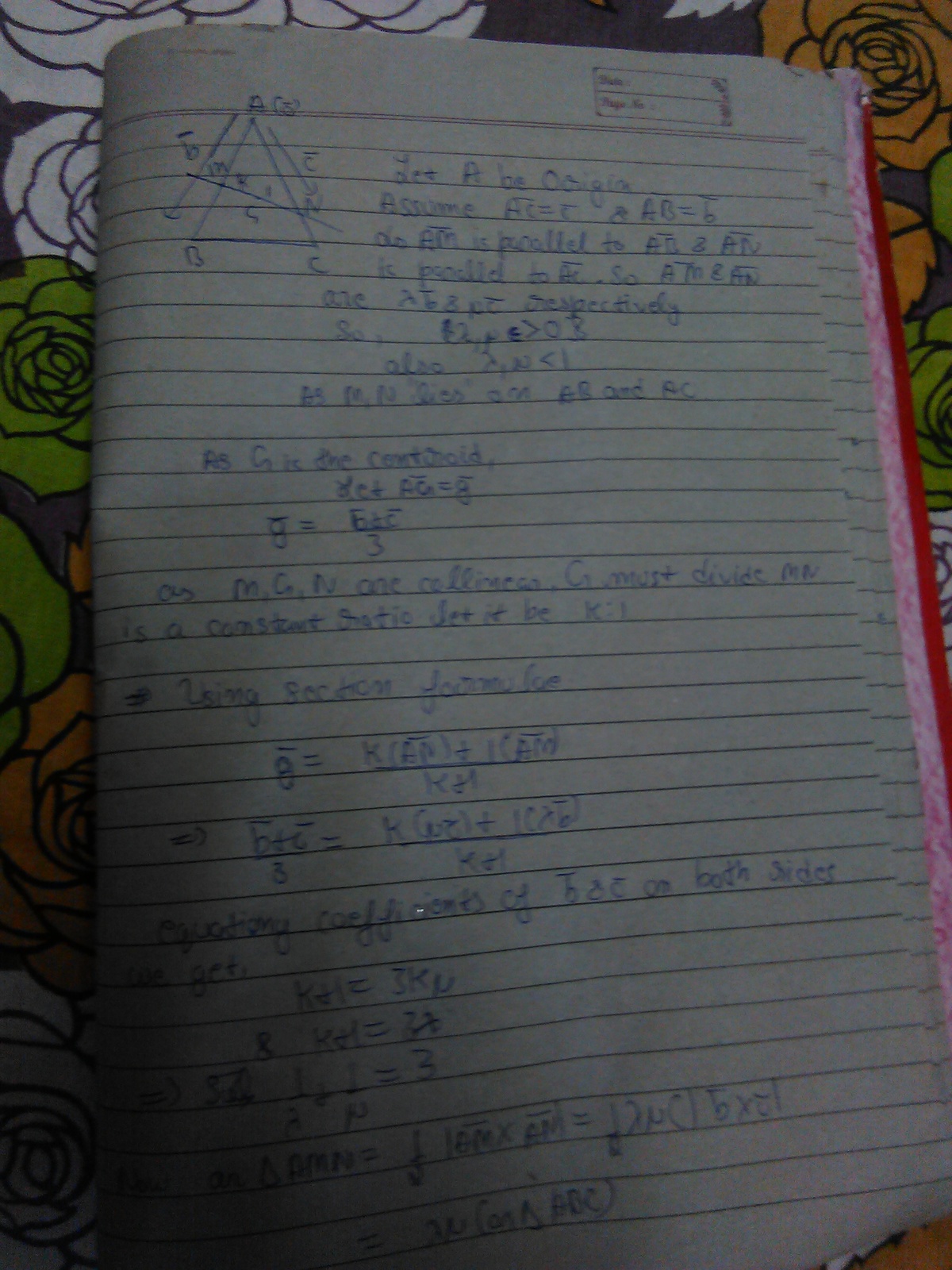
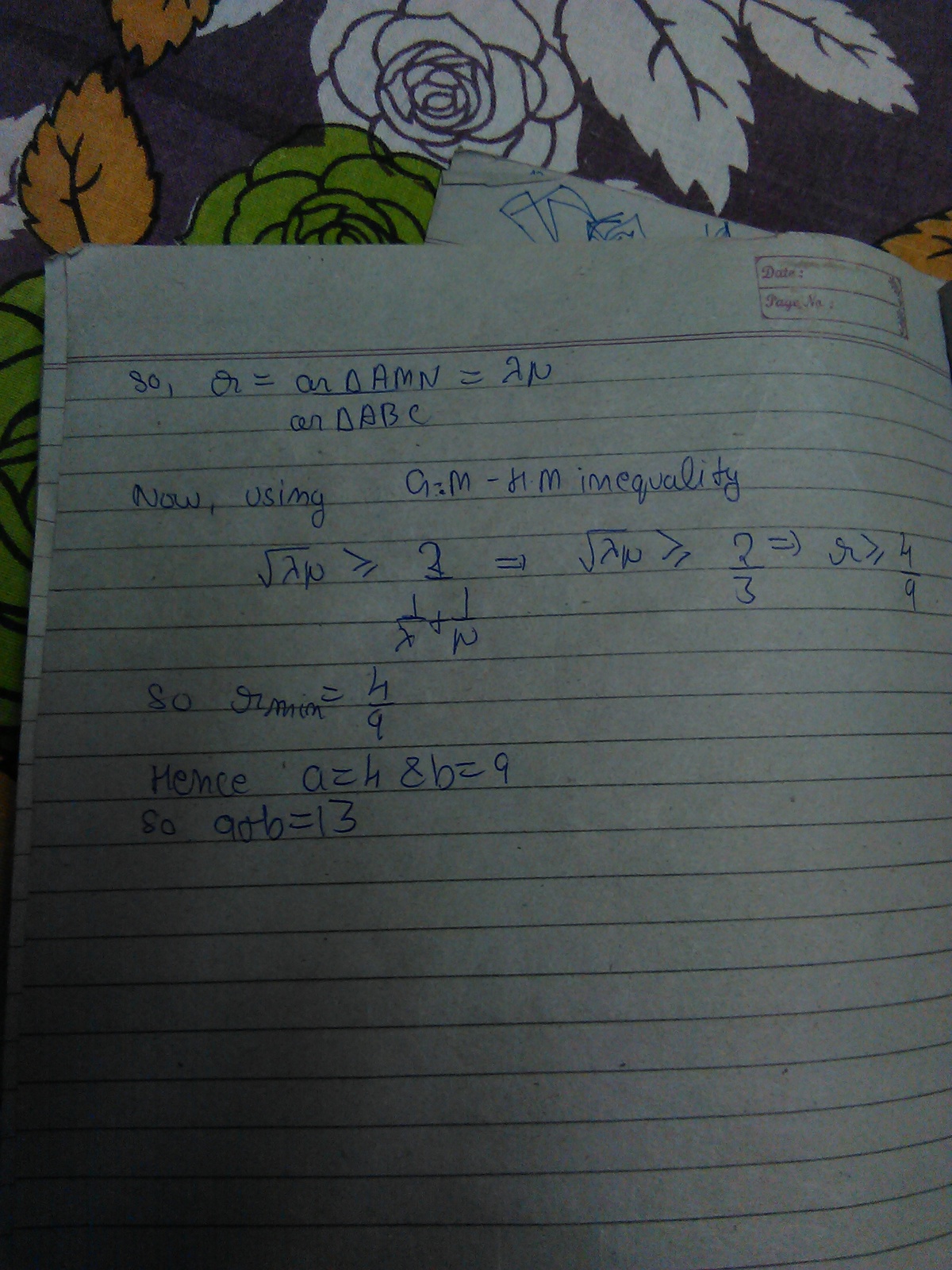
Area of PQR represented as [PQR].
Let line XGY || BC. Let D, E, F be midpoints of the sides as in the Fig.
AG/AD=2/3, so [AXY]/[ABC]=(2/3) * (2/3) =4/9..............(1)
Let M be between F and X. Then
[AMN]=[AXY] - [MGX] + [YGN]...........(2)
In triangle MGX and YGN, XG=GY, angle MGN= angle YGN.
It can be easily seen that MG < GN.
The product of two sides, and Sin of included angle in a triangle gives its area.
So [MGX] < [YGN].
So from (2), we get [AMN]>[AXY] for all M between F and X.
Similarly, when M is between B and X, N is between E and Y, we again get [AMN]>[AXY].
For M, G, N to be co-linear, M ca n be only between F and B.
So [AXY]=[AMN] is the minimum area. From (1) a/b=4/9. So a+b=4+9= 1 3 .