Triangles and circles?

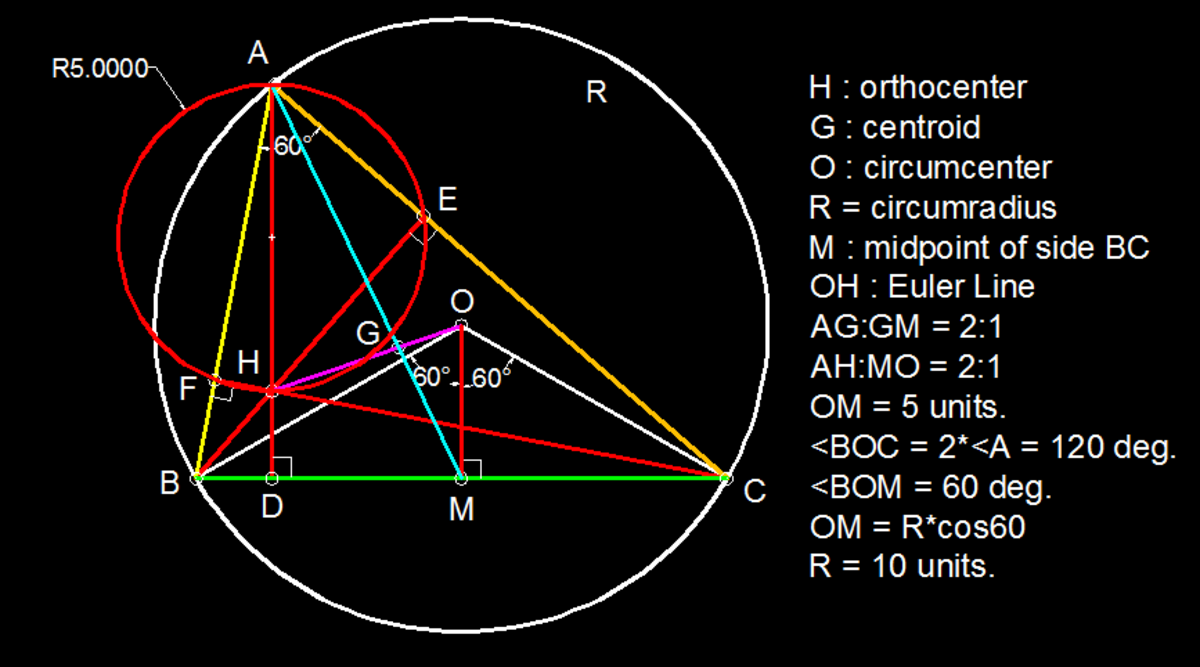
In quadrilateral, $AFOE \angle F + \angle E = 180^{\circ}$ . So this quadrilateral is cyclic.

Also since $\angle OFA = 90^{\circ}$ , $OA$ will be the diameter of the cyclic quadrilateral. Hence we can claim that $OA = 10$ units.

Now in $\Delta FCA$ :- $\angle FCA = 90^{\circ} - A$ $\sin \angle FCA = \dfrac{FA}{b}$ (Note that a,b,c and R have usual meanings). $\implies FA = b\cos A$ Now in $\Delta OFA$ :- $\angle FAO = 90^{\circ} - B$ $\cos \angle FAO = \dfrac{FA}{OA}$ $OA = \dfrac{b \cos A}{\sin B}$ Now we will use the result that $b = 2R \sin B$ . $OA = 2R \cos A$ $10 = 2 R \dfrac{1}{2}$ $R = 10 units$ Also $R$ is the circumradius of $\Delta ABC$ so the radius of required circle is $\boxed{10}$ .

Since angle CAB = 60 deg, AF : AC = AE : AB = 1:2. Notice too that BFEC is cyclic. Hence, Triangle AEF is similar to triangle ABC with ratio 1:2. Thus, the sides of triangle ABC are all twice the same as those of triangle AEF, and the area of the former is four times the same as the latter. By circumradius formula (where R = abc/4L; a, b, and c stand for the lengths of the sides of the triangle, L for area), the circumradius of ABC is double ((2 x 2 x 2)/4 = 2) of that of AEF. Hence, the answer.

Triangle AFC, angles at A and F are 60 and 90 so angle FCA =30.
Similarly angle EBA =30.
Triangle EOC, angles at C and E are 30 and 90 so angle EOC =60
So Angles OBC + CBO=60.
Because of symmetry, OBC=CBO=30. So triangle ABC is equilateral. (I will try to have a better reason.)
In the circle AFOE, angle AFO=90, so AO=10 the diameter. But O is also the circuncenter . So the required radius is 10.

Assume the triangle is equilateral, because you can. AO is equal the the circumradius of ABC, thus 10.