Blazing interpretation
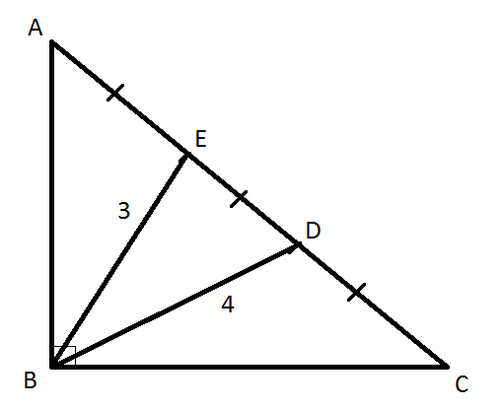
In triangle A B C , ∠ B = 9 0 ∘ , B E = 3 , and B D = 4 .
If A E = E D = D C , then the value of A C can be expressed as a b , where a and b are positive integers and b is square-free.
Find a + b .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
did the same way!!
Exactly same way.
How did you get 23???
Solve this pair of equations to find A B and B C
( 3 2 A B ) 2 + ( 3 1 B C ) 2 = 3 2
( 3 1 A B ) 2 + ( 3 2 B C ) 2 = 4 2
to get A B = 2 3 , B C = 3 3 , which then leads to A C = 3 5
Sir you can just add those equations to get
9 5 A B 2 + 9 5 B C 2 = 2 5 .
9 5 A C 2 = 2 5
Then A C = 3 5
Log in to reply
we can just take center of AC to be the origin. Then if AC is d then a circle passing through ABC has radius as d/2. E=[d/6,0] and D[-d/6,0] . using this and equation of circle and finding distances EB and DB gives AC as required.
Can you explain how did you get this pair of equations?
Log in to reply
Coordinate Geometry. Take B as origin. A as (0,y); C as (x,0)
Which theory
let F be the midpoint of DE and AE=ED=CD = X then , BF = 3X/2 as in a right angle triangle median on hypotenuse is half of it. now use stewarts theorem in traingle BED considering BF to be the cevian and solve for x
From Apollonius' Theorem , we get
A B 2 = 2 + 2 E D 2 __(1)
B C 2 = 2 3 + 2 E D 2 __(2)
Add both equations we get
9 E D 2 = 2 5 + 4 E D 2
E D = 5
Which gives C A = 3 5 ~~~