Triangles in a Circle

Call any meeting of two chords a vertex. A vertex on the circle is called external. Suppose that we start with $n\ge6$ points on the circle, so $n$ external vertices.

(a) There are ${}^nC_3$ triangles formed by $3$ external vertices.

(b) There are $4\times{}^nC_4$ triangles formed by $2$ external (and $1$ internal) vertices (we need to choose four external vertices - two to become vertices of the triangle, and two to be the other ends of the chords which intersect to form the other internal vertex - and there are $4$ ways of splitting any choice of four vertices so that two of them become the vertices of the triangle, with the other two forming the other ends of the chords).

(c) There are $5\times{}^nC_5$ triangles formed with $1$ external (and $2$ internal) vertex (we need to choose $5$ external vertices - one to be the external vertex in the triangle, two to be the other ends of the chords which connect to that vertex, and two to form the third chord that intersects the other two to form the two internal vertices - and there are $5$ ways of deciding which of the five vertices will be the external vertex of the triangle; the roles of the other four vertices is then determined).

(d) There are ${}^nC_6$ triangles formed with no external (and $3$ internal) vertices (we have to choose $6$ external vertices to be the endpoints of the three chords that intersect each other to form the three vertices of each triangle, and there is only one which in which six vertices can be connected with three chords to form a triangle).

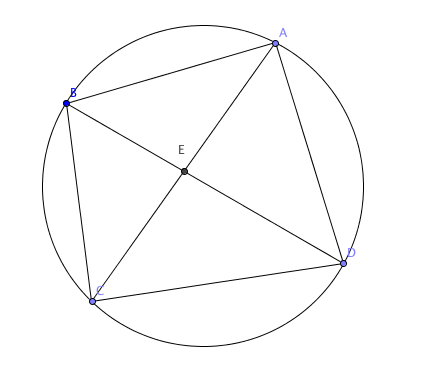
Thus there are ${}^n C_3 + 4\times {}^n C_4 + 5\times {}^n C_5 + {}^n C_6$ triangles altogether. When $n=8$ , this gives the answer $644$ .

Consider a triangle with vertices are $A,B,C$ .

Case 1 : Both $A,B,C$ are given points, we have $\binom{8}{3}$ triangles.

Case 2 : $A,B$ are given points, $C$ is the intersection of 2 chords, then $A,B$ and the other 2 end points of the chords intersect at $C$ are 4 of the given points. In reverse, if we choose 4 of the given points, 4 triangles of this kind are formed. Therefore, in this case, we have $4\binom{8}{4}$ triangles.

Case 3 : $A$ is a given points, $B,C$ are intersections of chords. The chord which contains $BC$ has two end points are 2 of the given points, say $D,E$ , which are different from $A$ . 2 chords which contain $AB,AC$ have one common end point is $A$ , the other 2 end points differ from each other, $A$ and $D,E$ . In reverse, if we choose 5 of the given points, there are 5 triangles of this kind for each way. Therefore, there are $5 \binom{8}{5}$ triangles of this kind.

Case 4 : Both $A,B,C$ are the intersections of chords. 6 end points of 3 chords are 6 of the given points and they are different. In reverse, with each way to choose 6 of the given points, we have exactly one triangle $ABC$ with vertices are the intersections of chords. In this case, we have $\binom{8}{6}$ triangles.

In conclusion, we have $\binom{8}{3} + 4\binom{8}{4} + 5\binom{8}{5} + \binom{8}{6} = 644$ triangles

We can do casework on the number of vertices of the triangle lie on the circle (and are one of the original 8 points).

Case 1: 0 vertices lie on the circle

In this case, 6 points of the eight must be chosen, and 3 chords must be drawn from the 6 points. None of the vertices will be on the circle since the chords don't share endpoints. We know that the three chords must all intersect, and with a little experimentation (I can't add pictures) we see the chords must connect opposite points, and since no three chords intersect at one point, this will produce a triangle. Each set of 6 points will give one triangle, so this case has $\dbinom{8}{6}=28$ possible triangles.

Case 2: 1 vertex on the triangle

Consider any one point $A$ and let that be our vertex on the circle. To have two vertices not on the circle, we must have 4 other points joined. $A$ must connect to two of the points ( $B$ and $C$ ), and the other two must be connected (call this chord $l$ ), and a triangle will be formed iff $A$ is not on the same side of $l$ as $B$ and $C$ . This forms a shape similar to an 'A' (draw it for yourself). Each set of 5 points can produce 5 triangles, since any point can be $A$ , so there are $\dbinom{8}{5}\cdot 5=280$ possibilities in this case.

Case 3: Two vertices are on the circle

In this case, we have two vertices on the circle ( $A$ and $B$ ), and one not. This means we must have 4 points chosen to connect chords. Also, the other two points must be on the same side of $\overline{AB}$ , since otherwise we don't have a triangle. Each set of 4 points gives 4 triangles (draw a quadrilateral and the diagonals; there is one triangle for each side) so there are $\dbinom{8}{4}\cdot 4=280$ possibilities in this case.

Case 4: All three vertices are on the circle

It is easy to see that any three points form one triangle (connect them), so this case holds $\dbinom{8}{3}=56$ possibilities.

The answer is $28+280+280+56=\boxed{644}$ .

We can count the triangles by first choosing the number of points in the circle that will form the triangle.

With 3 points there is 1 way. With 4 points there are 4 ways. With 5 points there are 5 ways. With 6 points there is 1 way.

Then the total is: $\binom{8}{3} + \binom{8}{4}*4 + \binom{8}{5}*5 + \binom{8}{6} = \boxed{644}$

You can see that these triangles can be classified this way: 3 vertex on the circle, 2 vertexes on the circle, 1 vertex or none. These are ALL the triangles you can count, and also , you do not repeat any 1 if u know how to count them ( which shouldn t be to hard). For those with 3 vertexes on the circle, the solution is trivial. When you have 2 vertexes on the circle: this type of triangle is defined by 4 random vertexes(actually 4 triangles of this type are determined by 4 random vertexes) When you have 1 vertex on the circle, u need 5 points in order for your triangle to be well determined(also, 5 point determine 5 triangles). I leave the case of triangles with no vertexes on the circle as a homework :)