Triangles in a Complete Graph
A
straight-line drawing
of a graph
is a drawing of
on the plane such that all its edges are straight line segments.
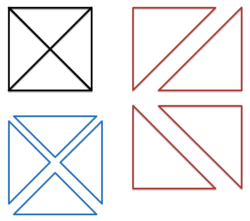
The maximum number of triangles that can be found in a straight-line drawing of the complete graph is 8, as seen in the image. For , there can be up to 35 triangles.
What is the maximum number of triangles that can be found in a straight-line drawing of the complete graph ?
The answer is 2430.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
We have four cases to consider based on the triangle's vertices.
Case 1: All vertices are vertices of G . In this case, there are simply ( 3 1 0 ) = 1 2 0
Case 2: Two vertices are vertices of G . In this case, the last vertex can be determined by the intersection of two diagonals, which means it can be determined with 4 points. Thus, there are ( 4 1 0 ) ways. However, we can choose any two consecutive points in the 4 points as the other two vertices, bringing the total up to 4 ⋅ ( 4 1 0 ) = 8 4 0
Case 3: One vertex is a vertex of G . In this case, the two vertices are determined with the intersection of a separate diagonal with two diagonals coming out of the one vertex that is a part of G , so this case can be determined with 5 vertices, or ( 5 1 0 ) ways. However, we can orient the one vertex that has two diagonals coming from it as any of the 5 vertices, giving the total to be 5 ⋅ ( 5 1 0 ) = 1 2 6 0
Case 4: No vertex is a vertex of G . In this case, the triangle can be determined by 6 vertices by connecting opposite vertices together with a diagonal. In this case there are ( 6 1 0 ) = 2 1 0 ways.
In total, there are 1 2 0 + 8 4 0 + 1 2 6 0 + 2 1 0 = 2 4 3 0 triangles.