Triangles In Rectangles
Consider the rectangle below, whose length is twice its height. If the three outer triangles shaded blue, yellow, and red have areas 2, 3, and 4 as shown, what is the area of the remaining inscribed green triangle?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
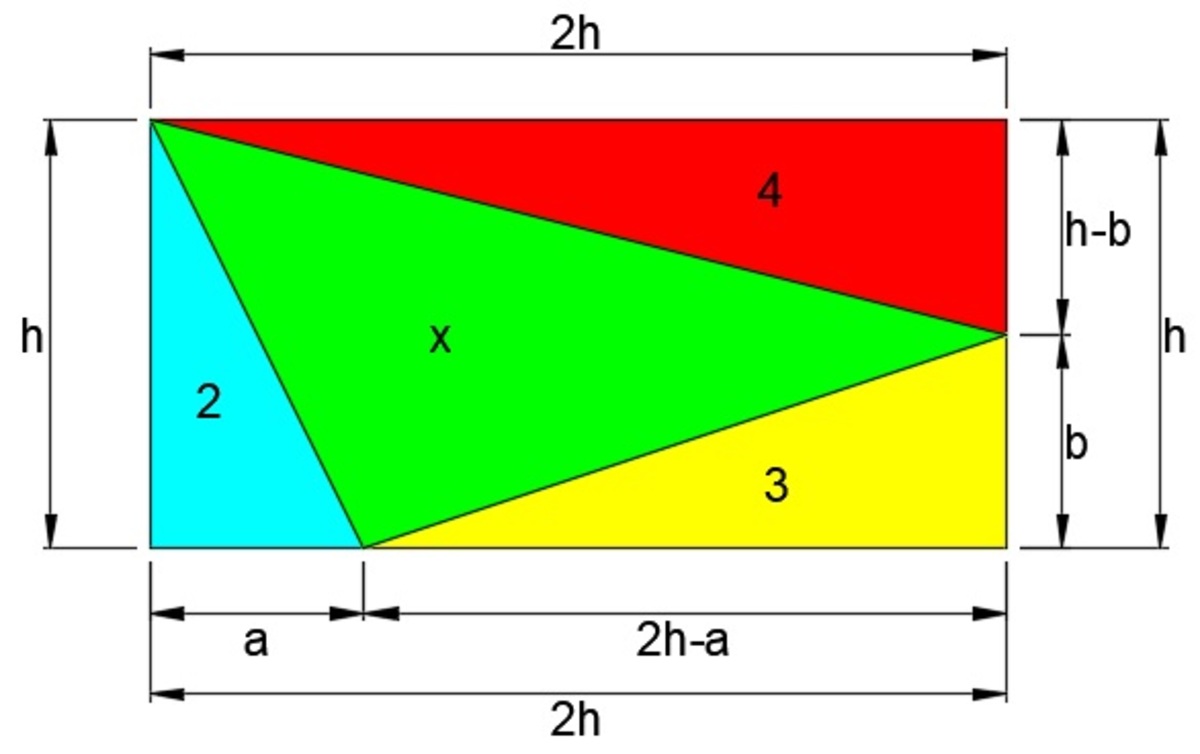 Consider my diagram. We know that the area of a triangle is
2
1
×
b
a
s
e
×
h
e
i
g
h
t
. Considering the blue triangle, we have
Consider my diagram. We know that the area of a triangle is
2
1
×
b
a
s
e
×
h
e
i
g
h
t
. Considering the blue triangle, we have
2 = 2 1 a h
a = h 4 ( E q . 1 )
Considering the yellow triangle, we have
3 = 2 1 ( 2 h − a ) b
6 = 2 h b − a b ( E q . 2 )
Considering the red triangle, we have
4 = 2 1 ( h − b ) 2 h
8 = 2 h 2 − 2 b h
4 = h 2 − b h ( E q . 3 )
Substitute ( E q . 1 ) in ( E q . 2 ) to solve for b , we get
b = h 2 − 2 3 h ( E q . 4 )
Substitute ( E q . 4 ) in ( E q . 3 ) then simplify, we get
h 4 − 9 h 2 + 8 = 0
Let y 2 = h 4 , then y = h 2 . So
y 2 − 9 y + 8 = 0
Solving for y by any method yields y = 8 and y = 1 . It is obvious that we must use y = 8 .
So
h 2 = y = 8 .
The area of the rectangle is h ( 2 h ) = 2 h 2 . Substituting the value of h 2 , we get
A = 2 h 2 = 2 ( 8 ) = 1 6
Let x be the area of the green region, then
1 6 = 2 + 3 + 4 + x
x = 1 6 − 9 = 7
From the areas of the blue and red triangles, we have that α x = 4 and 2 β x = 8 , so α = β .
Then from the area of the yellow triangle, we have
( x − β ) ( 2 x − α ) ( x − α ) ( 2 x − α ) 2 x 2 − 3 α x + α 2 2 x 2 − 3 ( 4 ) + ( x 4 ) 2 2 x 2 − 1 8 + x 2 1 6 x 4 − 9 x 2 + 8 ( x 2 − 8 ) ( x 2 − 1 ) x = ± 2 2 , ± 1 = 6 = 6 = 6 = 6 [Using α x = 4 ] = 0 = 0 = 0
x cannot be negative or 1 (as that would make the entire rectangle's area 2 ) so the only possible solution is x = 2 2 .
Then the area of the rectangle is 2 x 2 = 1 6 , so the area of the green triangle is 1 6 − 4 − 3 − 2 = 7
Using the picture above, we can construct an equation for the area of the rectangle as such:
Rectangle - A r e a = 2 h 2
Using the area of the rectangle as shown above, we can express the area of the inscribed green triangle as such:
Green Triangle - A r e a o f R e c t a n g l e − ( A r e a o f B l u e + R e d + Y e l l o w T r i a n g l e s ) => 2 h 2 − 9
Now that we have these two equations, we can express the areas of the three outer triangles shaded blue, red, and yellow as such:
Blue Triangle - 2 a h = 2 => a h = 4
Red Triangle - 2 2 b h = 4 => 2 b h = 8 => b h = 4
As proved above whilst simplifying the equations of the area of the red and blue triangles above, a h = 4 and b h = 4 . Therefore, a h = b h => a = b . Keep this in mind as we construct the equation for the area of the last outer triangle .
Yellow Triangle - 2 ( 2 h − a ) ( h − b ) = 3 => ( 2 h − a ) ( h − b ) = 6 => 2 h 2 − a h − 2 b h + a b = 6
At this point, remembering what we proved earlier is crucial when solving this problem. Again, since a = b , we can substitute a for b as such:
Yellow Triangle - 2 h 2 − a h − 2 ( a ) h + a ( a ) = 6 => 2 h 2 − a h − 2 a h + a 2 = 6 => 2 h 2 − 3 a h + a 2 = 6
Once again, recalling what we proved above is necessary to continue this problem. We proved a h = 4 , so we can substitute 4 for a h as such:
Yellow Triangle - 2 h 2 − 3 ( 4 ) + a 2 = 6 => 2 h 2 − 1 2 + a 2 = 6 => 2 h 2 + a 2 = 1 8 => 2 h 2 = 1 8 − a 2
At this point in the problem, it seems as if nothing else can be done to meaningfully get somewhere. However, if we observe the final equation for the area of the yellow triangle carefully, as well as consider the equation for the area of the green triangle , we can substitute as such:
Yellow Triangle - 2 h 2 − 9 = 9 − a 2 => ( A r e a o f G r e e n T r i a n g l e ) = 9 − a 2
Now, we have successfully derived two distinct equations for the area of the green triangle that we can set equal to each other as shown above: 2 h 2 − 9 as well as 9 − a 2 . However, having a minimum of one variable is critical to solving this problem. Using what we proved earlier that a h = 4 , we can deduce that h = a 4 , substitute a 4 for h , and simplify .
Green Triangle - 2 ( a 4 ) 2 − 9 = 9 − a 2 => 2 ( a 2 1 6 ) − 9 = 9 − a 2 => 2 ( a 2 1 6 ) + a 2 − 9 = 9 => 2 ( a 2 1 6 ) + a 2 = 1 8 => 2 ( 1 6 ) + a 4 = 1 8 a 2 => a 4 + 3 2 = 1 8 a 2 => a 4 − 1 8 a 2 + 3 2 = 0
Now that we have fully simplified the new equation illustrating the area of the green triangle , we can observe that it is a polynomial equation that can be solved by the quadratic formula as such where a = 1 , b = − 1 8 , and c = 3 2 :
Green Triangle - 2 ( 1 ) ( 1 8 ) + / − ( − 1 8 ) 2 − 4 ( 1 ) ( 3 2 ) => 2 1 8 + / − 3 2 4 − 1 2 8 => 2 1 8 + / − 1 9 6 => 2 1 8 + / − 1 4
At this point, there are two potential solutions for a 2 , so we need to list them both as well as substitute them into the original equation 9 − a 2 .
Solution 1 - 2 1 8 + 1 4 = a 2 => 2 3 2 = a 2 => 1 6 = a 2 => a = 4
Solution 2 - 2 1 8 − 1 4 = a 2 => 2 4 = a 2 => 2 = a 2 => a = 2
Now that we have solved for a 2 's two possible solutions, it's time to substitute .
Solution 1- 9 − ( 4 ) 2 = A r e a o f G r e e n T r i a n g l e => 9 − 1 6 = A r e a o f G r e e n T r i a n g l e => − 7 = A r e a o f G r e e n T r i a n g l e
Solution 2- 9 − ( 2 ) 2 = A r e a o f G r e e n T r i a n g l e => 9 − 2 = A r e a o f G r e e n T r i a n g l e => 7 = A r e a o f G r e e n T r i a n g l e
Since only one of the two potential solutions is positive , the answer that the A r e a o f t h e G r e e n T r i a n g l e = 7 is the correct answer .