Triangles in Semicircle

What is the area of the largest triangle that we can inscribe in a semicircle of radius 1? One of the sides of the triangle has to lie on the diameter.
Once you solve this, try this related problem
The answer is 1.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
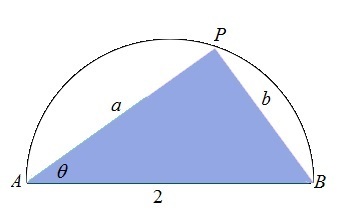
Let A P = a , B P = b and ∠ P A B = θ . We know that angle extended in a semicircle ∠ A P B = 2 π . Then the area of the triangle inscribed in the semicircle is given by A = 2 1 a b = 2 1 ( 2 cos θ ) ( 2 sin θ ) = sin 2 θ . A is maximum, when sin 2 θ is maximum, that is sin 2 θ = 1 , and A m a x = 1 .
Here,
A= .5* base* height
A = .5 * 2 * 1
A=1.00
Base = 2 * radius
Height = radius
Treating the area of the triangle as 1/2 X base X height,
we know that the maximum base is the entire diameter, which has length 2,
and the maximum height is to the top of the semicircle, which is the entire radius of length 1.
Hence, the maximum area is 2 1 × 2 × 1 , which is achieved by the triangle with vertices ( − 1 , 0 ) , ( 0 , 1 ) , ( 1 , 0 ) .
Now, the reason for creating this problem, is that it allows us to easily solve the following question
It is very well-known that the largest rectangle is a square. The goal is to obtain a proof that follows as a corollary of my question. If you want a hint of how to prove that, check out the related problem .