Triangles in the grid
How many triangles can you make using points on this 5 × 5 square grid as their vertices?
Note : Some of the triangles can be congruent, and they can overlap one another.
Three possible triangles are shown.
The answer is 2148.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Two errors here even though the final answer is correct.
You missed accounting for 4 lines of length 3 (they are parallel to the blue lines but closer to the corners.) So there are a total of 16 lines of length 3.
Your final calculation should be 2 3 0 0 − 1 2 ∗ 1 0 − 4 ∗ 4 − 1 6 ∗ 1 = 2 1 4 8
Yes, I worked it out the same way. However, surely triangles that have zero area are also triangles? It didn't specify in the question so I originally entered 2300, which is the correct answer with the question how it is, and then worked out for just non-degenerate triangles
Log in to reply
Yes maybe It has to say "non-degenerate" triangles but it is left as obbyess. If it wasn't like that then it wouldn't be an Advanced.
If degenerate triangles are allowed then your answer is still wrong since you also need to consider the situations where two or more points are the same. Thus you would have to add the 25 triangles based on a single point and the 25 * 24 = 600 triangles where two vertices are the same and the third is distinct, to give 2925 in total.
Log in to reply
n choose r doesn't allow the same thing to be chosen twice, it takes it into account
line with 3 lenght is difficult to find totally
here triangle can be made using more points than 3. why only choosing 3? I.don't get that
Why oh why oh why do these questions have to be so tedious...
For three points to not form a triangle, they must be colinear, so we'll count how many ways there are to choose 3 colinear points, and subtract that from the number of ways to choose 3 points without any conditions. To do this, we'll consider every possible line in which the 3 points can be:
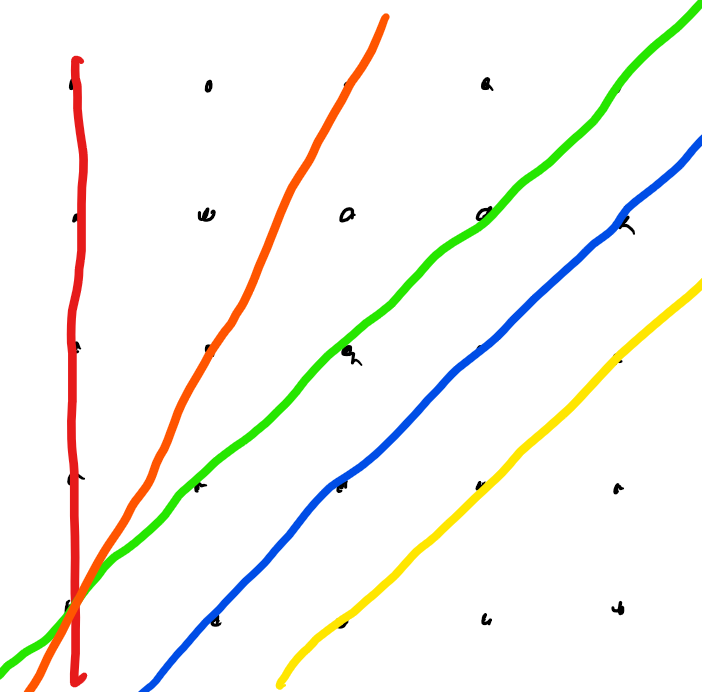
In the red line, there are ( 3 5 ) = 1 0 ways to pick 3 points, and there are 1 0 "similar" lines ( 5 horizontal, and 5 vertical)
In the green line, again, there are ( 3 5 ) = 1 0 ways to pick 3 points, and there are 2 similar lines (each one is a diagonal)
For the blue line, there are ( 3 4 ) = 4 ways, for the green line there is ( 3 3 ) = 1 , and there are 4 similar lines to each of those ( 2 parallel to each diagonal of the square)
Finally, for the orange line, there is ( 3 3 ) = 1 way to pick 3 points, and there are 1 2 of those ( 3 with slope 2 , 3 with slope − 2 , 3 with slope 2 1 and 3 with slope 2 − 1 )
This makes our total
1 0 ⋅ 1 0 + 2 ⋅ 1 0 + 4 ⋅ ( 4 + 1 ) + 1 2 ⋅ 1 = 1 5 2
There are ( 3 2 5 ) = 2 3 0 0 ways to pick 3 points in the 5 × 5 grid, so the number of triangles is 2 3 0 0 − 1 5 2 = 2 1 4 8
Sweet,simple,perfect!
In the line about the blue and green lines, you mean the blue and yellow lines.
There are ( 3 2 5 ) = 2 3 0 0 ways to choose 3 points. We need to subtract from this the number of ways the 3 points would be colinear. We will count these by the point that is between the other two. There are 6 possible types of points that might be between the other two; A: the center, B: a unit distance from the center, C: one diagonal distance from the center, D: the midpoint of an edge, E: between the midpoint of an edge and its corner, and F: a corner. If we use the lowercase of a point to denote the number of colinear triplets with that point between the other two, our answer can be written as 2 3 0 0 − a − 4 b − 4 c − 4 d − 8 e − 4 f . It does not take long to calculate that f = 0 , e = 3 , d = 4 , c = 1 0 , b = 1 3 , a = 2 0 giving us the answer 2148.
I did this with brute force code after too much head-scratching. I wrote code with three nested FOR loops, one for each point of the triangle, each loop running through the possible 25 positions.
Inside the inner loop I calculated the area formed by every possible combination of three points in the grid and if non-zero, I added it to a counter.
Finally, I divided the total count by 6, as there are 6 possible orders that each valid triangle can be formed by three points. (ABC, ACB, BAC, BCA, CAB or CBA).
In order for a triangle to exist, it must be defined by three points. Thus, we can find the total number of triangles by finding the number of ways to choose three points out of the 25 total points. This is equal to ( 3 2 5 ) = 2 3 0 0 .
But of course, this includes the many degenerate triangles that occur when the three chosen points are collinear. In order to find the actual number of triangles, we must subtract the many sets of three collinear points. In order to do this, we can use more counting methods:
First, note that there are ten lines of five points each, five horizontal lines and five vertical lines. Then, the two major diagonals are also lines with 5 points. In a single line of five points, there are ( 3 5 ) ways of choosing 3 collinear points. In total, this is 1 2 ⋅ ( 3 5 ) = 1 2 0
Now let's look at lines with four points. There are only four of them (they all have slopes 1 or − 1 ). Each line contains ( 3 4 ) collinear dots of three. In total, this makes 4 ⋅ ( 3 4 ) = 1 6
Finally, there are the lines of length three. Again, there are four of these with slopes 1 or − 1 . However, there are also many triples of points that make lines with slopes 2 1 , 2 , 2 − 1 , or − 2 . In total, this adds 12 more lines or 16 total lines made of three dots. This means 1 6 ⋅ ( 3 3 ) = 1 6
Altogether then, the total number of degenerate triangles made of three collinear points is 1 2 0 + 1 6 + 1 6 = 1 5 2 .
Subtracting from the total number of ways to choose three points, 2 3 0 0 − 1 5 2 = 2 1 4 8
Thus, 2 1 4 8 triangles can be made by using three points on a 5 × 5 square grid.
There are ( 3 2 5 ) or 3 ∗ 2 ∗ 1 2 5 ∗ 2 4 ∗ 2 3 which is 2300 ways to choose 3 points in a 5 by 5 grid. However, there could be points in a straight line like this:
So, we must find how many such combinations there are on one line.
Now, we must find the total number of each type of line.
For lines with length 5, there are 12 total lines (5 horizontal, 5 verticle, 2 diagonal)
For lines with length 4, there are a total of 4 llines (4 diagonal)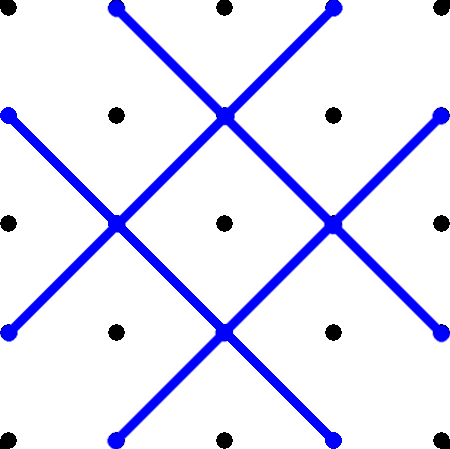
For lines with length 3, there are a total of 16 (4 through the center, 8 through the points directly horizontal or vertice from the center, 4 on the edges)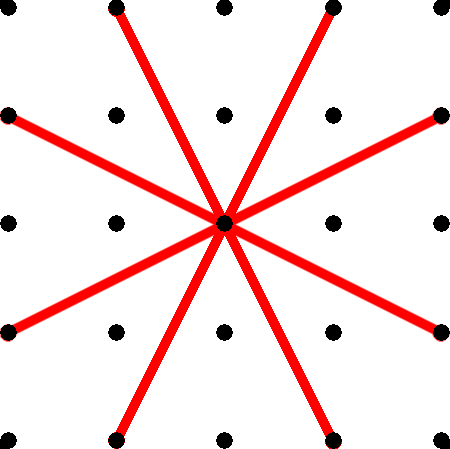
That gives us a total of 2 3 0 0 − 1 2 ∗ 1 0 − 4 ∗ 4 − 1 6 ∗ 1 = 2 1 4 8 total triangles