Triangles in Triangles in Triangles...
 What is the largest natural number
such that we can NOT subdivide an equilateral triangle into
, not necessarily congruent, equilateral triangles?
What is the largest natural number
such that we can NOT subdivide an equilateral triangle into
, not necessarily congruent, equilateral triangles?
Examples:
-
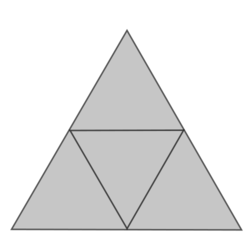
We CAN subdivide an equilateral triangle into 4 equilateral triangles like in the image above.
- But we can NOT subdivide an equilateral triangle into 2 (possibly different) equilateral triangles.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The answer is 5 . Here is a non-rigorous and lazy solution. Enjoy!
We'll show you can make subdivide our equilateral triangle into 6 , 7 and 8 not necessarily congruent equilateral triangles and then show that you cannot subdivide it into 5 .
Part 1: Subdividing Equilateral Triangles into 6 , 7 and 8 necessarily congruent equilateral triangles .
Suppose we have an equilateral triangle with each side of length a . Here's how to subdivide it into 6 , 7 and 8 respectively :
Disclaimer : I didn't have a ruler or compass on me when drawing these images (what am I doing with my life?)!
Part 2: Showing that If I can subdivide into K triangles I can subdivide into K + 3 .
Suppose we can subdivide an equilateral triangle into K not necessarily congruent equilateral triangles. Then we can also subdivide an equilateral triangle into K + 3 not necessarily congruent equilateral triangles by making one of our subdivided triangles into 4 like so :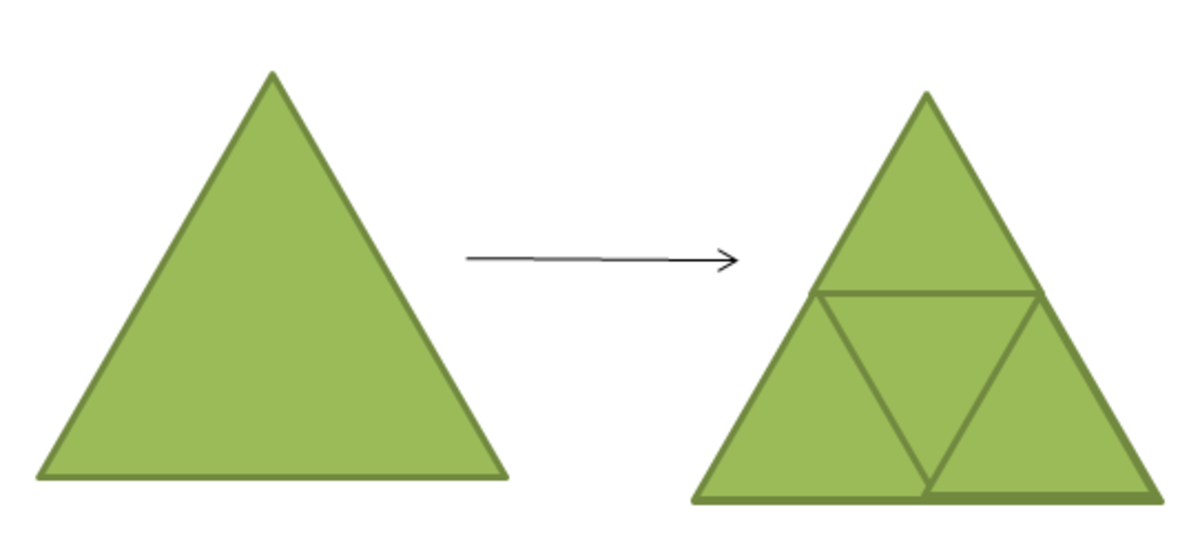
Using the cases K = 6 , 7 , 8 from before and this information we can prove by induction on K that we can make every K ≡ 0 m o d ( 3 ) , K ≡ 1 m o d ( 3 ) , K ≡ 2 m o d ( 3 ) for all K ≥ 6 .
Part 3: Finishing up.
Now we've shown we can subdivide for all for all K ≥ 6 it suffices to show that we can NOT do so for K = 5 . I'm not going to show that here (at least not yet! ) but hopefully you can prove for yourselves that this is not possible. If you can post it for everyone to see!