Triangles inside a square
is a square and
is a point inside it so that
and angle
is 15 degrees. What is the magnitude of angle
in degrees?
Bonus: Try solving without the use of trigonometry.
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
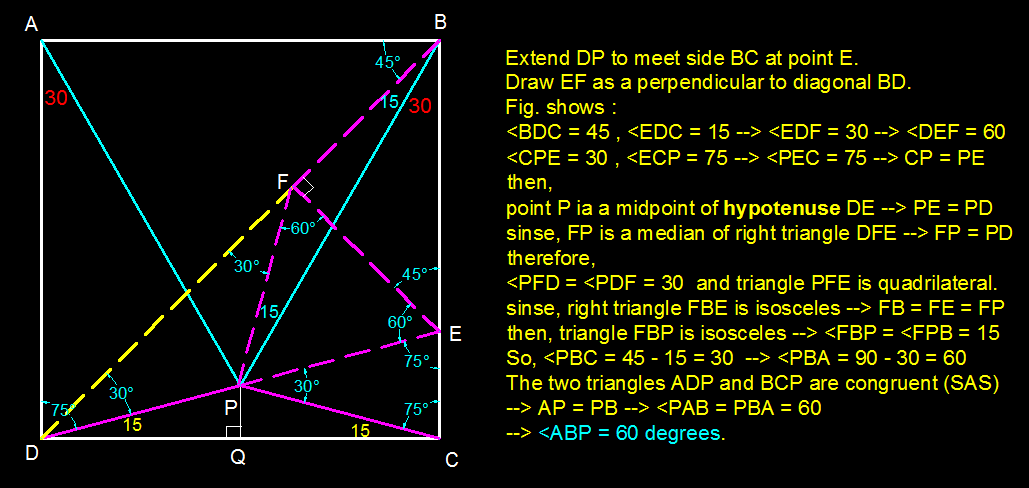
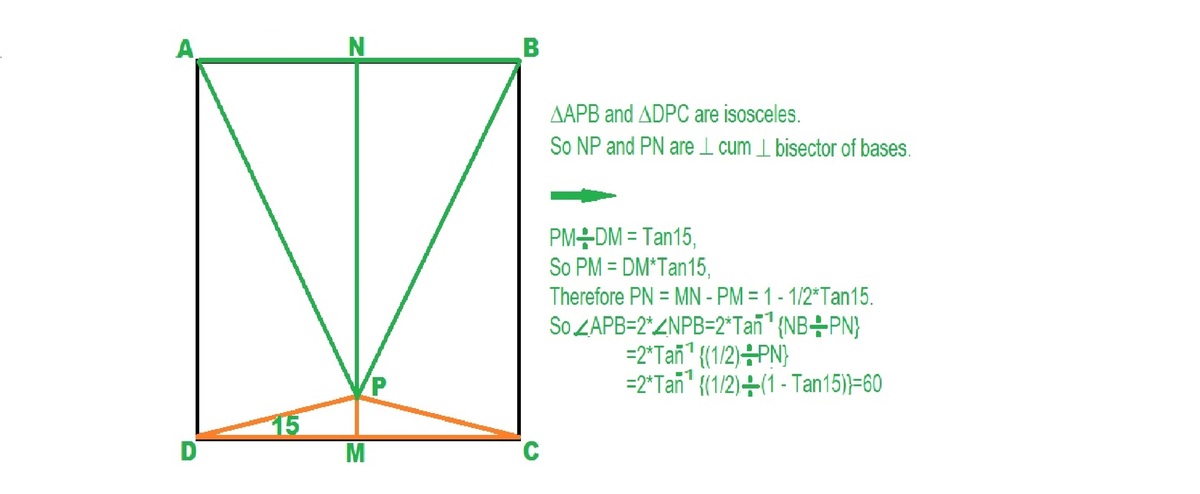
One way is to draw a line parallel to BC through P and solve using trigonometry. But to do it geometrically, the method of angle chasing doesn't seem to work. Hence we make use of inequalities:
First, call ang. APB as 'x' and deduce the other angles in terms of x as shown in the diagram. It is easily seen that triangle APB is isosceles with AP = BP
Now let's assume AP > AB, and noting that an angle opposite to a longer side in a triangle is larger than an angle opposite to a shorter side, we can say
ang. ABP > ang. APB
90 - x/2 > x
x/2 < 30
Reversing the signs and adding 105 to both sides we get:
105 - x/2 > 105 - 30
105 - x/2 > 75
ang. APD > ang. ADP which must mean that AD > AP
Since we began with the assumption that AP > AB, this must mean AD > AP > AB which is impossible because AD and AB are sides of a square and hence must be equal.
Making the exact opposite assumption as the one we made earlier i.e. assuming AP < AB, we can show in exactly the same way that it leads to AD < AP < AB which is again impossible because AD = AB.
As AP > AB and AP < AB are both impossible, then the only other option is AP = AB which makes the triangle APB equilateral.
Thus, ang. APB = x = 60 degrees