Triangles on a Christmas tree

I found a bijective solution which I thought I would share. More generally, suppose that we have a triangular grid with $n$ points along each side. Let the three corners of the grid be $X$ , $Y$ , and $Z$ . Let $S$ be the set of points consisting of the $n$ points along edge $YZ$ , along with two other points $A$ and $B$ . (The exact locations of $A$ and $B$ are not important; we are just adding them in order to form a set containing $n + 2$ points.)

Then the number of equilateral triangles in the grid is equal to $\binom{n + 2}{4}.$ We will prove this by constructing a bijection between the equilateral triangles in the grid and the subsets of $S$ of size four.

If we choose a subset of $S$ of size four, then it will fall into one of the following cases:

Case 1 : The subset contains two points on edge $YZ$ , and $A$ and $B$ .

Let $P$ and $Q$ be the two points on edge $YZ$ . For this subset, we take the equilateral triangle with base $PQ$ .

https://i.imgur.com/VP1O2DH.png

Case 2 : The subset contains three points on edge $YZ$ , and $A$ .

Let $P$ , $Q$ , and $R$ be the three points on edge $YZ$ , in that order. Draw the line through $P$ that is parallel to $XY$ , and the line through $R$ that is parallel to $XZ$ ; let them intersect at $U$ . Next, draw the line through $Q$ that is parallel to $XZ$ ; let it intersect $UP$ at $V$ . Finally, let the line through $V$ that is parallel to $YZ$ intersect $UR$ at $W$ . For this subset, we take equilateral triangle $UVW$ .

https://i.imgur.com/rpY5gzU.png

Case 3 : The subset contains three points on edge $YZ$ , and $B$ .

Let $P$ , $Q$ , and $R$ be the three points on edge $YZ$ , in that order. Draw the line through $P$ that is parallel to $XY$ , and the line through $R$ that is parallel to $XZ$ ; let them intersect at $U$ . Take points $V$ and $W$ on $UP$ and $UR$ , respectively, so that $UV = PQ = RW$ . For this subset, we take equilateral triangle $QVW$ .

https://i.imgur.com/eSVGAD9.png

Case 4 : The subset contains four points on edge $YZ$ .

Let $P$ , $Q$ , $R$ , and $S$ be the four points on edge $YZ$ , in that order. Draw the line through $P$ that is parallel to $XY$ , and the line through $S$ that is parallel to $XZ$ ; let them intersect at $U$ . Draw the line through $Q$ that is parallel to $XY$ , and the line through $R$ that is parallel to $XZ$ ; let them intersect at $D$ . Draw the line through $D$ that is parallel to $YZ$ ; let it intersect $UP$ and $US$ at $V$ and $W$ , respectively. Finally, take points $E$ and $F$ on $UW$ and $UV$ , respectively, so that $DW = EU = FV$ . For this subset, we take equilateral triangle $DEF$ .

https://i.imgur.com/FxR9Sil.png

Thus, we have a bijection between the equilateral triangles in the grid and the subsets of $S$ of size four, so the number of equilateral triangles is $\binom{n + 2}{4}.$ For $n = 10$ , this number is $\binom{12}{4} = 495$ .

The curx of this proof is understanding how to form a tilted equilateral triangle. This is explained in "Case 2", especially with reference to the image.

---

Let's focus on the number of equilateral triangles that are added when we add on the nth row. We want to show that this is equal to ${ n + 1 \choose 3 }$ , from which the result follows.

We already have $n$ points in the base, and it makes sense to choose 3 from them. Let us add 1 more point, which I would call the "zero point". Now, let's explain what happens when we pick 3 points out of this set of $n + 1$ points.

Case 1: If it contains the "zero point",
then we just construct the obvious equilateral triangle which has the other 2 points as the base. For example, if we chose the 3 red points (where the point on the extreme right is the "point at infinity", then we will get the blue equilateral triangle.

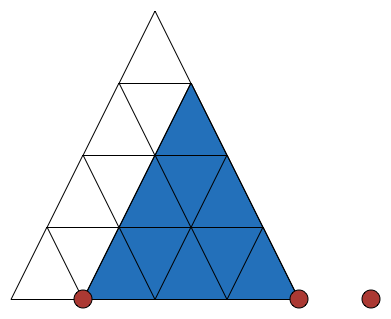
This establishes the injection onto equilateral triangles which contain 2 points on the base. It is obvious that this is a bijection.

Case 2: If all 3 points are within the $n$ points in the base,
Define the middle red point as the "pivot point". This will be the point of the triangle that touches the nth line.
We record the number of units away that the left and the right point are, as $l$ and $r$ respectively.
Then, for the left red point, we move it up and to the right by $r$ units, and mark this point left blue.
For the right red point, we move it up and to the left by $l$ units, and mark this point right blue.

As an explicit example, if the 3 red points where chosen as below, then we have the pivot, and blue points accordingly.

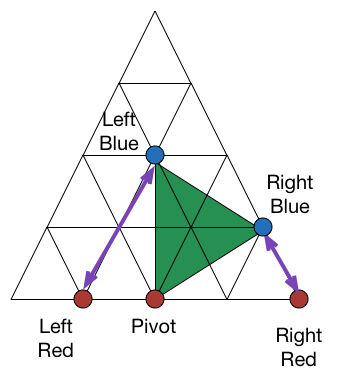
Claim: The two blue points and the pivot point form an equilateral triangle.

Proof: The distance between any blue point and the pivot point is equal to

$x = \sqrt{ l^2 + r ^2 - 2 lr \cos 60 ^ \circ }$

Consider the triangle with side lengths $x, l, r$ , where the angle between $l$ and $r$ is $60 ^ \circ$ , with vertices $X, L, R$ respectively. Then, the angle that left blue, pivot, left red makes is $\angle LRX$ , and the angle that the right blue, pivot, right red makes is $\angle RLX$ . This means that the angle that "left blue, pivot, right blue" makes is

$180 ^ \circ - \angle LRX - \angle RLX = \angle RLX = 60 ^ \circ$

Hence, we have an isosceles triangle which has a vertex angle of $60 ^ \circ$ , hence it is an equilateral triangle.

This establishes the injection onto equilateral triangles which contain a single point on the base.

Claim: We have a bijection. (I leave it to you to find the obvious inverse function, now that I've told you how to view these equilateral triangles.

Hence, this shows us that $T(n) - T(n-1) = { n+1 \choose 3 }$ , from which it follows that $T(n) = { n+2 \choose 4 }$ .

---

Note: I call it the "zero point", because Case 1 is actually a subset of Case 2, where we treat the "zero point" as the duplicate of the second point. Then, the second point is the pivot, the left point moves by 0 (hence stays on the base), and the right point (which is the "zero point") moves up to form the equilateral triangle.

Case 1 interpreted as Case 2:

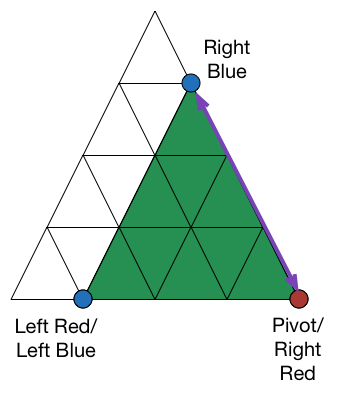
Note: One can, in a similar manner, create a bijection between $n+2$ points choosing 4 of them, and all equilateral triangles. The additional point determines the "height" of the lowest point of the triangle.
This slightly complicates the image, without adding too much value, so I left it out.

Great ideas Calvin Lin , Jon Haussmann , and Maria Kozlowska! I will present a different idea, which I hope you find interesting.

Denote an equilateral triangle lattice with $n$ rows by $T_n$ . Let $t_n$ be the number of distinct equilateral triangles that can be formed with vertices from $T_n$ . I will prove that the recurrence $t_n=3t_{n-1}-3t_{n-2}+t_{n-3}+n-1$ holds, and later deduce via a nice generating function that $t_n=\dbinom{n+2}{4}$ . The recurrence is easier to understand through example. For the sake of example, let $n=12$ . In the images below, either all three points of the triangle are within the red space, or there is at least one outside the red space.

Imgur

Imgur

Imgur

The only triangles that haven't been counted yet are the ones with all vertices on the border of the big triangle, and there are $n-1$ of those (convince yourself of this). Thus we have just established $t_n=3t_{n-1}+n-1$ , right? WRONG. We have some nasty over counts. The following regions are counted twice, but only need to be counted once, and thus we must subtract them each from the count once.

Imgur

Imgur

Imgur

Thus we have $t_n=3t_{n-1}-3t_{n-2}+n-1$ , right? STILL WRONG. Just one tiny under count now, though. Since it was added thrice and subtracted thrice, we must add it once more.

Imgur

Finally, our recurrence is established. We have $t_n=3t_{n-1}-3t_{n-2}+t_{n-3}+n-1$ with $t_0=t_1=0,t_2=1$ . Now we can use a nice generating function to get a closed form (for the problem though you can just bash out the recursion up to $t_{10}$ ). Let $G(x)=\sum_{n\geq 1} t_nx^n.$ From the recursion we can easily establish that $G(x)=3xG(x)-3x^2G(x)+x^3G(x)+\sum nx^n-\sum x^n.$ Recall from geometric series that $\sum x^n=\frac{x}{1-x}$ . Now let $F(x)=\sum nx^n=x+2x^2+3x^3+4x^4+\cdots$ so $xF(x)=x^2+2x^3+3x^4+\cdots.$ It follows from geometric series that $(1-x)F(x)=\frac{x}{1-x}\implies F(x)=\frac{x}{(1-x)^2}.$ Now we have from earlier $(1-3x+3x^2-x^3)G(x)=\frac{x}{(1-x)^2}-\frac{x}{1-x}.$ Miraculously, $1-3x+3x^2-x^3=(1-x)^3$ , hence $G(x)=\frac{x}{(1-x)^5}-\frac{x}{(1-x)^4}.$ It remains to compute the coefficient of $x^n$ . Note that $\frac{x}{(1-x)^5}=x(1+x+x^2+\cdots)(1+x+x^2+\cdots)(\cdots)(\cdots)(\cdots),$ so it's easy to form a bijection between the number of ordered quintuples of nonnegative integers that sum to $n-1$ and the coefficient of $x^n$ in $\frac{x}{(1-x)^5}$ . However, the former is well known to be $\dbinom{n-1+5-1}{5-1}=\dbinom{n+3}{4}$ . In the same manner, one can easily find the coefficient of $x^n$ in $\frac{x}{(1-x)^4}$ to be $\dbinom{k+2}{3}$ . A closed form is thus $\dbinom{k+3}{4}-\dbinom{k+2}{3}$ , which by Pascal's Identity is equal to $\boxed{\dbinom{k+2}{4}}$ .

After input from Brian, Jon and Calvin I wanted to present another three bijections. First, supporting one, to show how coordinates of any point in the area bounded by the triangle can be represented by two numbers $1 <= a < b <= n+1$ representing two points on a line below the triangle.

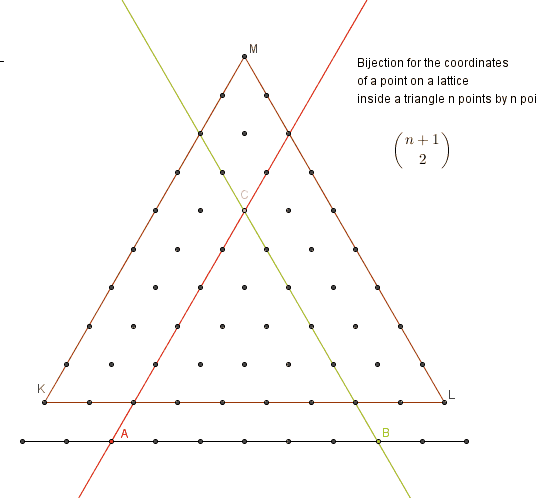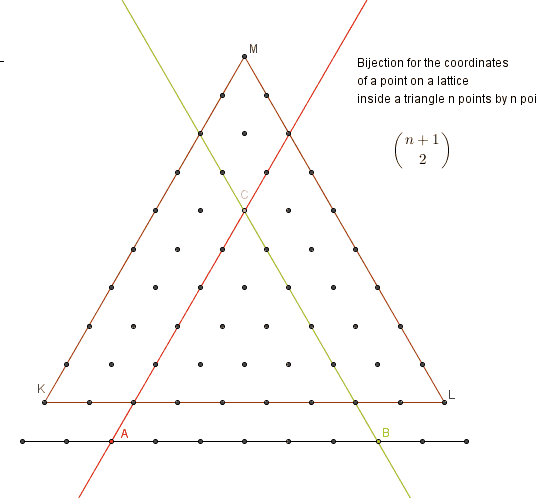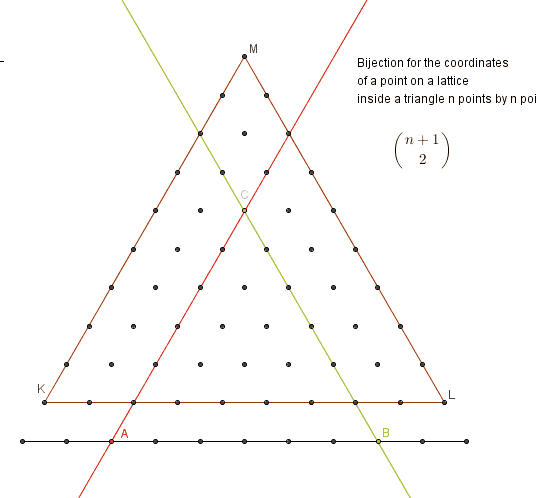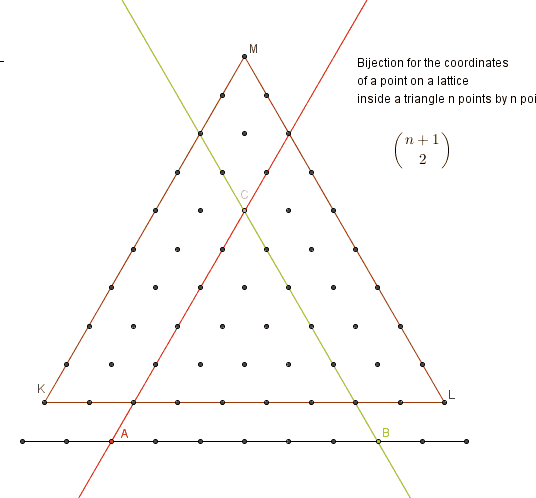
The second bijection is to show creation of triangles with at least one vertex on a base:

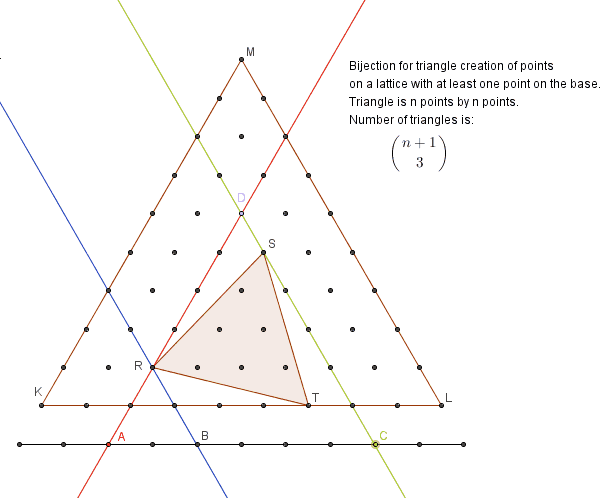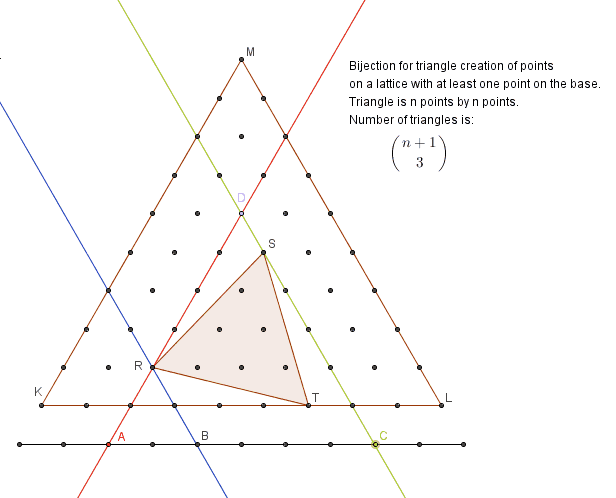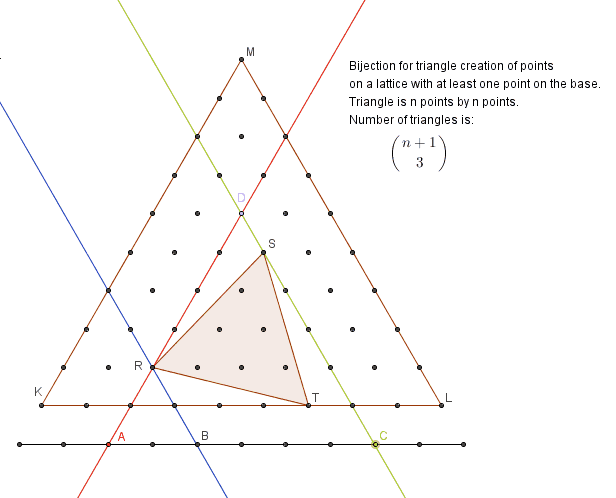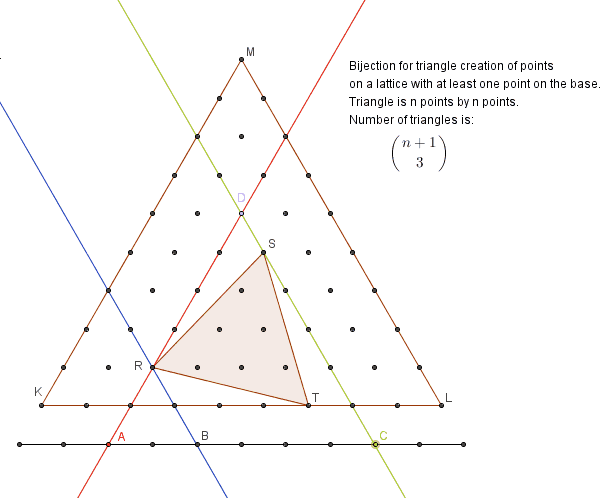
The third bijection is to show selection of any four points on a line of 12 points located two levels below the large triangle represents any equilateral triangle created from points of a bounded lattice.

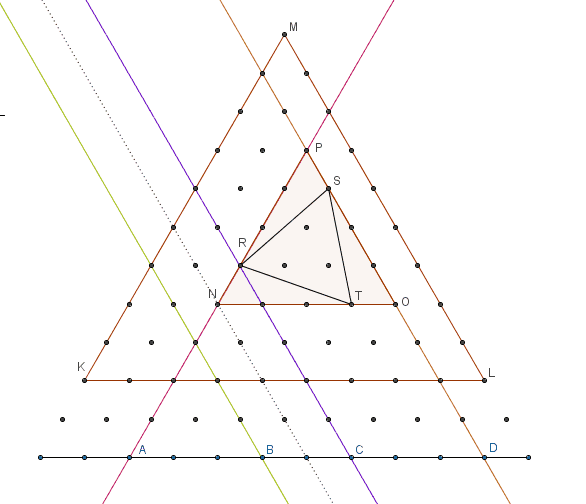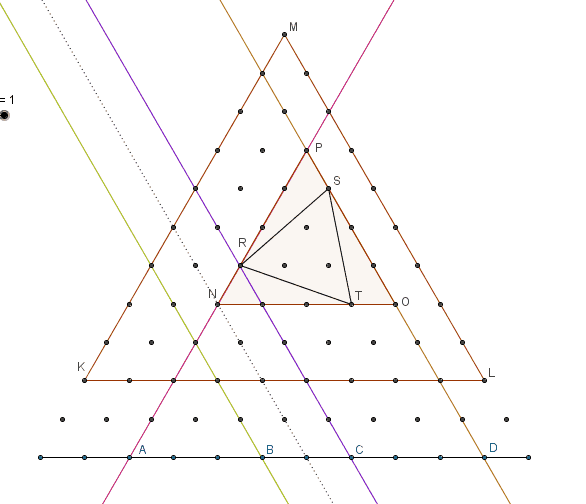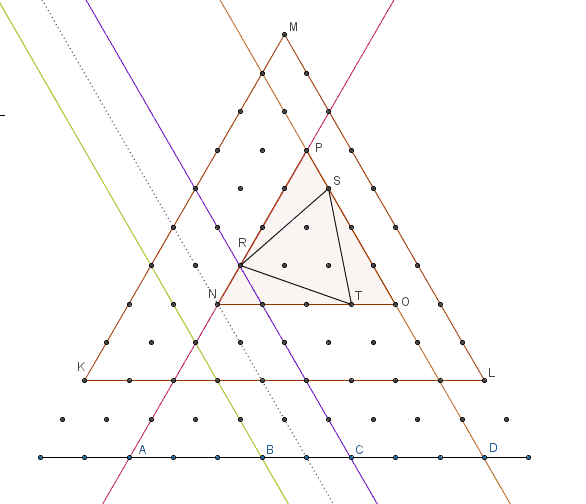
Numbers $1<=a<b<c<d<=12$ represent four points $A, B, C, D$ on a line. Lines through point $A \parallel MK$ and through $D \parallel ML$ intersect at point $P$ which will be top vertex of the circumscribing triangle.

Line through $B \parallel ML$ has a corresponding line created one unit above it which intersects line through $A$ at point $N$ . This creates circumscribing $\triangle NOP$ . Line through $c \parallel ML$ intersects line through $A$ at point $R$ . $\triangle RST$ is inscribed inside $\triangle NOP$ . For $c-b=1$ there is no tilt and $\triangle NOP = \triangle RST$ .

This establishes that number of triangles is $\binom{n + 2}{4} = \binom{12}{4}=495$

There is in fact a formula for this general problem, namely

$T_{n} = \dfrac{n(n + 1)(n + 2)(n + 3)}{24},$

where the equilateral triangular lattice has side "length" $n,$ (i.e., $(n + 1)$ points a side). (Note that the above formula has been adjusted for the offset given in the link.)

In this case we have $T_{9} = \dfrac{9*10*11*12}{24} = \boxed{495}.$