Triangles on a Hexagon
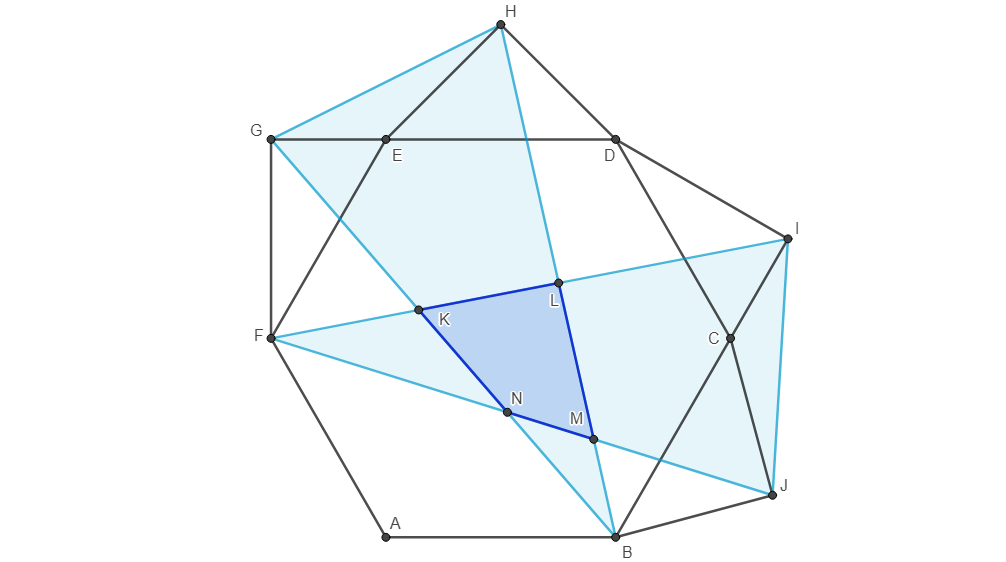 (To Scale)
(To Scale)
The diagram above shows a regular hexagon . Triangles and are 30-60-90 triangles. Triangles and are right isosceles triangles. The triangles and intersect to form quadrilateral . Find the ratio of the area of to the area of . Express your answer to the nearest thousandth.
The answer is 9.373.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let A be at ( 0 , 0 ) and let B be at ( 1 , 0 ) on the cartesian plane.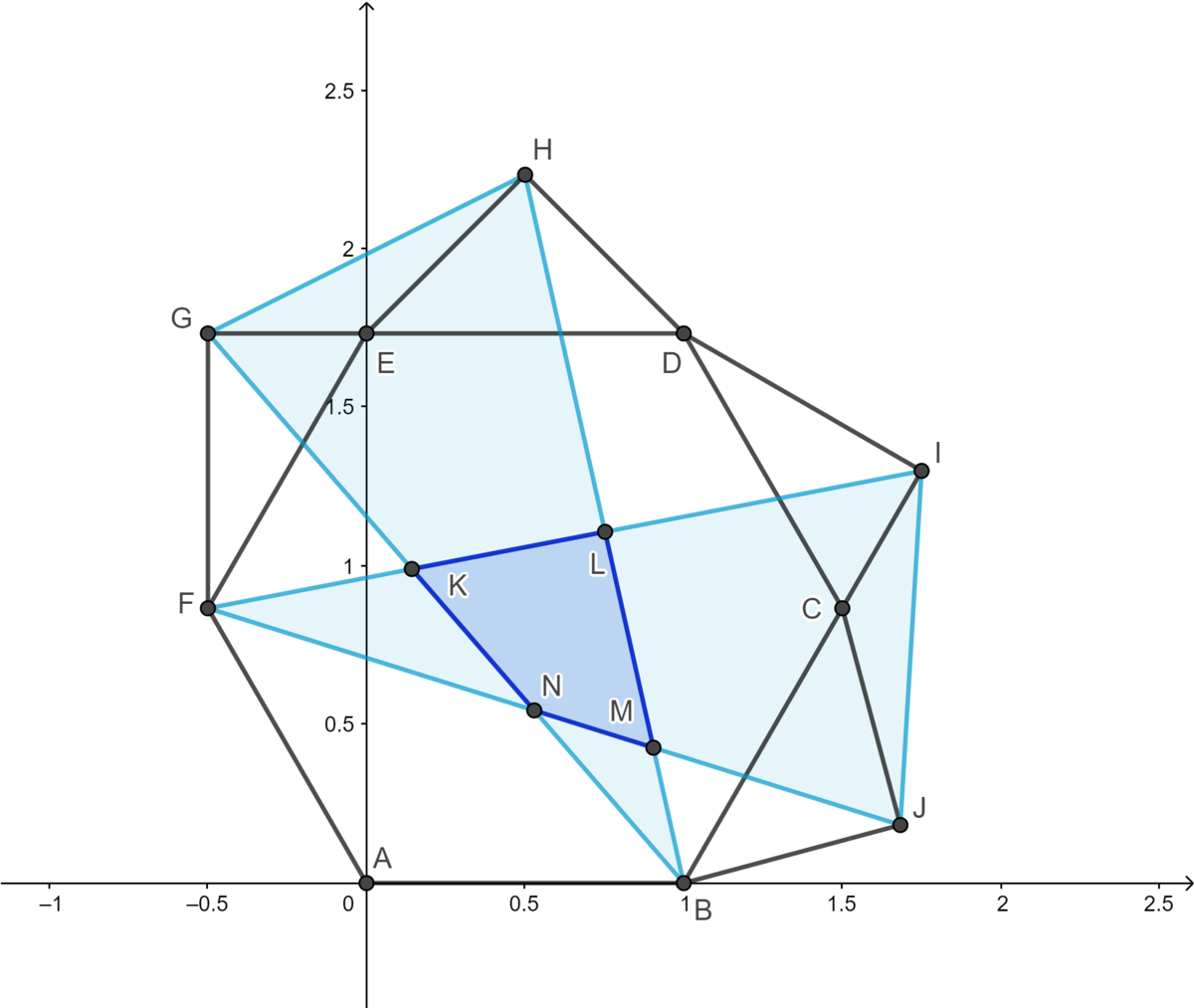 The cordinates of point
F
can be found by drawing perpendicular lines at points
F
and
A
to form a 30-60-90 triangle as shown.
The cordinates of point
F
can be found by drawing perpendicular lines at points
F
and
A
to form a 30-60-90 triangle as shown.
 Since the hypotenuse is of length 1, the shorter leg has length
2
1
and the longer leg has length
2
1
⋅
3
or
2
3
. This gives us the coordinates of
F
which are
(
−
2
1
,
2
3
)
.
The coordinates of
F
,
G
,
H
,
I
,
J
, and
B
can all be found using various methods using properties of 30-60-90 and 45-45-90 triangles and circles.
Since the hypotenuse is of length 1, the shorter leg has length
2
1
and the longer leg has length
2
1
⋅
3
or
2
3
. This gives us the coordinates of
F
which are
(
−
2
1
,
2
3
)
.
The coordinates of
F
,
G
,
H
,
I
,
J
, and
B
can all be found using various methods using properties of 30-60-90 and 45-45-90 triangles and circles.
The final coordinates (you'll have to take my word for it, or do it yourself) end up being the following.
B : ( 1 , 0 )
F : ( − 2 1 , 2 3 )
G : ( − 2 1 , 3 )
H : ( 2 1 , 3 + 2 1 )
I : ( 4 7 , 4 3 3 )
J : ( 4 ( 5 + 3 ) , 4 ( − 1 + 3 ) )
Using point-slope form gives us the equations for the lines H B , G B , I F , and J F .
H B : y = − 2 1 ( 3 + 2 1 ) ( x − 1 )
G B : y = − 2 3 3 ( x − 1 )
I F : y − 2 3 = 4 9 4 3 ( x + 2 1 )
J F : y − 2 3 = 4 ( 5 + 3 ) + 2 1 4 ( − 1 + 3 ) − 2 3 ( x + 2 1 )
We can solve these equations to find the points K , L , M , N .
K : ( 7 1 , 7 4 3 )
L : ( 1 6 7 9 3 + 1 1 0 , 1 6 7 3 ( 1 + 3 5 3 ) )
M : ( 3 7 2 ( 1 5 + 3 ) , 3 7 1 ( 1 2 3 − 5 ) )
N : ( 5 9 3 3 + 2 6 , 5 9 2 ( 1 1 3 − 3 ) )
The shoelace theorem is a useful theorem, which gives us the following. K L M N = 2 ∣ 7 1 ⋅ 1 6 7 3 ( 1 + 3 5 3 ) + 1 6 7 9 3 + 1 1 0 ⋅ 3 7 1 ( 1 2 3 − 5 ) + 3 7 2 ( 1 5 + 3 ) ⋅ 5 9 2 ( 1 1 3 − 3 ) + 5 9 3 3 + 2 6 ⋅ 7 4 3 − ( 7 4 3 ⋅ 1 6 7 9 3 + 1 1 0 + 1 6 7 3 ( 1 + 3 5 3 ) ⋅ 3 7 2 ( 1 5 + 3 ) + 3 7 1 ( 1 2 3 − 5 ) ⋅ 5 9 3 3 + 2 6 + 5 9 2 ( 1 1 3 − 3 ) ⋅ 7 1 ) ∣
This simplifies to K L M N = 2 5 5 1 9 2 7 3 9 0 7 8 9 + 5 9 1 1 6 1 3 .
The area of hexagon A B C D E F is equivalent to 6 times the area of an equilateral triangle with side length 1. A B C D E F = 6 ⋅ 4 3
The ratio of the areas of A B C D E F to K L M N is 2 5 5 1 9 2 7 3 9 0 7 8 9 + 5 9 1 1 6 1 3 6 ⋅ 4 3 or about 9.373088985.
Rounding to the nearest thousandth gives us 9 . 3 7 3 .