Triangles say it all
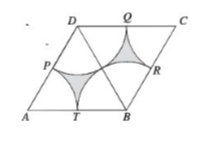 Let be
and
equilateral triangles of side
.
and
are middle points of
and (\triangle BCD.
Let be
and
equilateral triangles of side
.
and
are middle points of
and (\triangle BCD.
Find the shaded area.
The answer is 8.0627.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Solution 1:
First, calculate △ A D B and △ B D C areas, both triangles have equal areas.
base = 1 0
height = 2 1 0 3 (you can use trigonometry or phytagoras theorem to find it)
∣ △ A B D ∣ = 2 1 0 × 2 1 0 3 = 2 5 3
Second, calculate circular sector.
Put together the three circular sectors of △ A B D and you get a semi-circle of radii 5 . The area of this semi-circle is 2 2 5 π
Finally, shaded area is 2 × ( 2 5 3 − 2 2 5 π ) = 5 0 3 − 2 5 π ≈ 8 . 0 6 3
Solution 2:
A D C B is a parallelogram so its area is 1 0 × 2 1 0 3 = 5 0 3 .
The six circular sectors form a cirlce of radii 5 which area is 2 5 π
Shaded area is 5 0 3 − 2 5 π = ≈ 8 . 0 6 3