Triangles The Invaders!
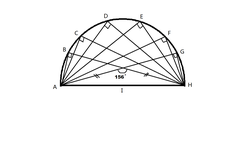 Help! "Semicircle" country is invaded by so many right-angled triangles!
The army of the "Semicircle" country need your help.
They said: "∠AJH=156° and AJ=JH. ∠BAG and ∠BHG are separated into 5 equal parts. Their weakest part is at ∠DAH. If we able to determine the angle, we could destroy them immediately!"
So, help them to determine ∠DAH.
Help! "Semicircle" country is invaded by so many right-angled triangles!
The army of the "Semicircle" country need your help.
They said: "∠AJH=156° and AJ=JH. ∠BAG and ∠BHG are separated into 5 equal parts. Their weakest part is at ∠DAH. If we able to determine the angle, we could destroy them immediately!"
So, help them to determine ∠DAH.
The answer is 51.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since triangle A J H is isosceles, ∠ J A H = ∠ J H A = 1 2 .
Since ∠ A J H and ∠ B J A are supplementary, ∠ B J A = 2 4 ,
Since ∠ B J A and ∠ B A J are complementary (they are the non-right angles of right triangle B A J ), ∠ B A J = 6 6 .
Since ∠ B A J = ∠ B A G is divided in 5 equal parts, and ∠ D A J is 5 3 of ∠ B A J , ∠ D A J = 3 9 . 6 .
∠ D A H = ∠ D A J + ∠ J A H = 3 9 . 6 + 1 2 = 5 1 . 6 .