Triangular Area
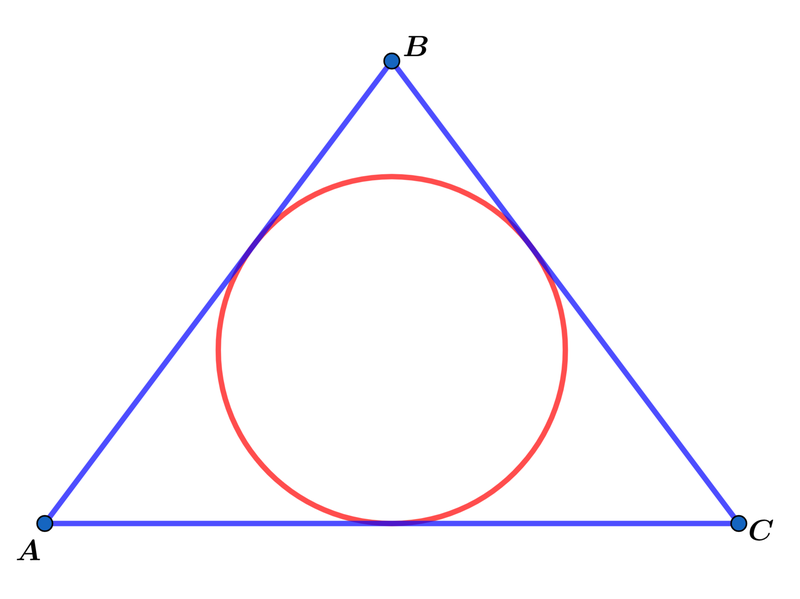
In the diagram above △ A B C is an isosceles triangle with ∣ A B ∣ = ∣ B C ∣ = ∣ A C ∣ − 1 . If the radius of the inscribed circle is 2 3 , find the area of △ A B C .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the base length of the isosceles triangle be a , then the leg length is a − 1 . Then its height of triangle h = ( a − 1 ) 2 − ( 2 a ) 2 = 2 ( 3 a − 2 ) ( a − 2 ) and its area A = 4 a ( 3 a − 2 ) ( a − 2 ) . Since the incircle of the triangle has a radius of 2 3 , the area is also given by A = 4 3 ( 3 a − 2 ) . Therefore,
4 a ( 3 a − 2 ) ( a − 2 ) a a − 2 a 3 − 2 a 2 a 3 − 2 a 2 − 2 7 a + 1 8 ( a − 6 ) ( a 2 + 4 a − 3 ) = 4 3 ( 3 a − 2 ) = 3 3 a − 2 = 2 7 a − 1 8 = 0 = 0 Squaring both sides
⟹ a = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 6 7 − 2 − 7 − 2 ⟹ A = 4 3 ( 3 ( 6 ) − 2 ) = 1 2 ⟹ A < 0 Unacceptable ⟹ A < 0 Unacceptable
I decided to use an area approach here.
The height h of isosceles △ A B C is h = ( x − 1 ) 2 − ( 2 x ) 2 = 2 3 x 2 − 8 x + 4
⟹ The area A △ A B C = 2 1 x h = 4 3 x 2 − 8 x + 4 ∗ x
and A △ A B C can also be expressed as A △ A B C = A △ A P C + A △ A P B + A △ B P C
= 4 3 ( 3 x − 2 )
⟹ 3 ( 3 x − 2 ) = 3 x 2 − 8 x + 4 ∗ x ⟹ 9 ( 3 x − 2 ) 2 = ( x − 2 ) ( 3 x − 2 ) ( x 2 ) ⟹ ( 2 − 3 x ) ( x 3 − 2 x 2 − 2 7 x + 1 8 ) = 0 ⟹ ( 2 − 3 x ) ( x − 6 ) ( x 2 + 4 x − 3 ) = 0
( x 2 + 4 x − 3 ) = 0 ⟹ x = 7 − 2 (dropping the negative root) and
x = 7 − 2 ⟹ ∣ A B ∣ = 7 − 3 < 0 ∴ x = 7 − 2 is not a valid solution to the problem.
x = 3 2 ⟹ ∣ A B ∣ < 0 ∴ x = 3 2 is not a valid solution to the problem.
Using x = 6 ⟹ ∣ A C ∣ = 6 , ∣ A B ∣ = ∣ B C ∣ = 5 and height h = 4 ⟹
A △ A B C = 1 2 .