Triangular Electric Field
Find the electric field due to a equilateral triangle plate of side ℓ and charge density σ at a distance 4 1 ℓ 3 2 above centroid up to 4 decimal places. σ = 1 0 − 9 C m − 2 , ϵ 0 = 8 . 8 5 × 1 0 − 1 2 F m − 1 .
The answer is 28.2485.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
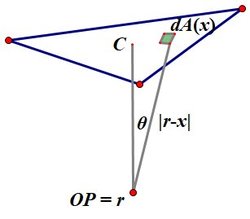 The electric field at a point
P
with position vector
r
is
E
=
4
π
ε
0
σ
∬
T
∣
r
−
x
∣
3
r
−
x
d
A
(
x
)
where the integral is over the triangle
T
. By symmetry, the electrc field at the particular point
P
will be normal to the triangle, and so we calculate
E
=
4
π
ε
0
σ
C
P
∬
T
∣
r
−
x
∣
3
d
A
(
x
)
k
=
4
π
ε
0
σ
∬
T
∣
r
−
x
∣
2
cos
θ
d
A
(
x
)
k
=
4
π
ε
0
σ
∬
T
d
Ω
(
x
)
k
=
4
π
ε
0
σ
Ω
k
where
C
is the centroid of the triangle,
Ω
is the solid angle subtended by the triangle
T
at the point
P
and
k
is a unit vector in the direction of
P
C
. Now
P
is at the centroid of a regular tetrahedron of which
T
is one of the faces. Thus, by symmetry,
Ω
=
4
1
×
4
π
=
π
, and hence
E
=
4
ε
0
σ
k
and, with the given values of
σ
and
ε
0
, we have
∣
E
∣
=
2
8
.
2
4
8
6
.
The electric field at a point
P
with position vector
r
is
E
=
4
π
ε
0
σ
∬
T
∣
r
−
x
∣
3
r
−
x
d
A
(
x
)
where the integral is over the triangle
T
. By symmetry, the electrc field at the particular point
P
will be normal to the triangle, and so we calculate
E
=
4
π
ε
0
σ
C
P
∬
T
∣
r
−
x
∣
3
d
A
(
x
)
k
=
4
π
ε
0
σ
∬
T
∣
r
−
x
∣
2
cos
θ
d
A
(
x
)
k
=
4
π
ε
0
σ
∬
T
d
Ω
(
x
)
k
=
4
π
ε
0
σ
Ω
k
where
C
is the centroid of the triangle,
Ω
is the solid angle subtended by the triangle
T
at the point
P
and
k
is a unit vector in the direction of
P
C
. Now
P
is at the centroid of a regular tetrahedron of which
T
is one of the faces. Thus, by symmetry,
Ω
=
4
1
×
4
π
=
π
, and hence
E
=
4
ε
0
σ
k
and, with the given values of
σ
and
ε
0
, we have
∣
E
∣
=
2
8
.
2
4
8
6
.
This is just 1/4 of flux of a tetrahedron (due to guess law). So sigma/4€o