Triangular numbers

With $T_n = \tfrac12n(n+1)$ we obtain $\begin{aligned} S_N & = \; \sum_{j=1}^N T_j T_{N+1-j} \; = \; \tfrac14\sum_{j=1}^N j(j+1)(N+1-j)(N+2-j) \\ & = \; \tfrac14\sum_{j=1}^N j(j+1)\Big[(j+2)(j+3) - 2(N+4)(j+2) + (N+3)(N+4)\Big] \\ & = \; \tfrac14\left(\begin{array}{l}\tfrac15N(N+1)(N+2)(N+3)(N+4) - 2(N+4) \times \tfrac14N(N+1)(N+2)(N+3) \\+ (N+3)(N+4) \times \tfrac13N(N+1)(N+2)\end{array}\right) \\ & = \; \tfrac14\big(\tfrac15 - \tfrac12 + \tfrac13\big)N(N+1)(N+2)(N+3)(N+4) \\ & = \; \tfrac{1}{120}N(N+1)(N+2)(N+3)(N+4) \; = \; \binom{N+4}{5} \end{aligned}$ The question asks about $S_{101} \; =\; \binom{105}{5} \; = \; 96560646$ making the last five digits $\boxed{60646}$ .

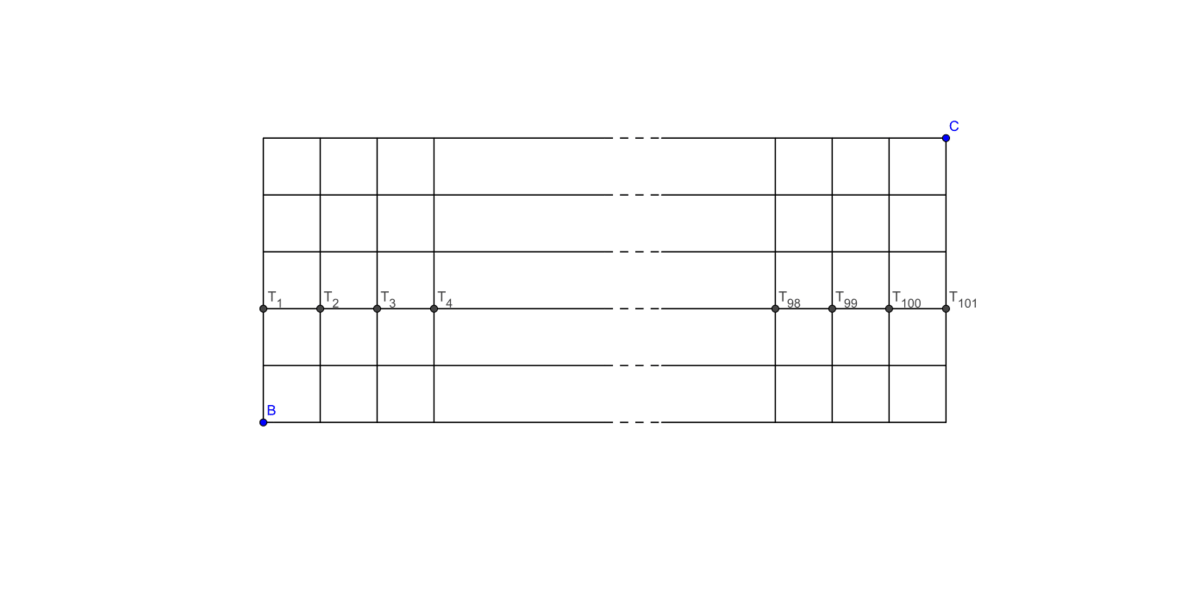
I'll use a double counting technique in order to get the number of ways to go from $B$ to $C$ using $\uparrow$ and $\rightarrow$ movements.

Clearly the total number of ways to go from $B$ to $C$ in a rectangle of 5x100 is $\binom{100+5}{5} = \binom{105}{5}$

On the other hand, we are able to "manipulate" the pathway counting separately the ones which pass through $T_1$ and immediately after make a $\uparrow$ movement, the ones which pass through $T_2$ and immediately after make a $\uparrow$ movement and so on until $T_{100}$ : then, it suffices to sum up all the different paths.

• Paths which pass trough $T_1$ and immediately after make a $\uparrow$ movement : they are made of all the pathways which start from $B$ to $T_1$ and all the ones which start from $T_1$ to $C$ . So they are $\binom{0+2}{2} \cdot \binom{100+2}{2} = T_1 \cdot T_{101}$
• Paths which pass trough $T_2$ and immediately after make a $\uparrow$ movement : as the previous case they are $\binom{1+2}{2} \cdot \binom{99+2}{2} = T_2 \cdot T_{100}$

and so on. So, $\sum_{i=1} ^{101} T_i T_{102-i} = T_1 T_{101} + T_2 T_{100}+...+T_{101} T_1 = \binom{105}{5} = 96,560,646$ The answer is $\boxed{60646}$