Triangular numbers and pascal's triangle
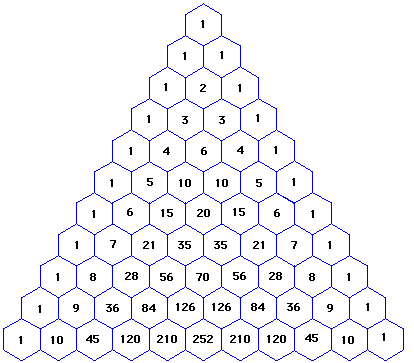 Looking at pascal's triangle from left to right, find the 2013th number on the 2015th row of pascal's triangle.
Looking at pascal's triangle from left to right, find the 2013th number on the 2015th row of pascal's triangle.
Consider the very top row as the 1st row.
The answer is 2027091.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
Or... u can use binomial theorem like what Abdullah Shahriar did.
you gave a clear explanation ,it is easy to understand
Each n row has n numbers. In row 2015 there are 2015 numbers. The 2013'th number will be the 3rd from the right. Notice that starting in row 3, the 3rd number from right gives an arithmetic series, basically row 3: 1, row 4: 1 + 2, row 5, 1 + 2 + 3, and so on. In row 2015, 3rd number from the right, you will have the sum (1+2+3...+2012+2013). Using the formula for sum of an arithmetic series, (1+an)(n/2), (1+2013)/(2013/2) = 2027091. The 2013 as n is obtained because the pattern starts in row 3, or 2 rows late, so 2015-2 = 2013
For any row k, the n t h element (from either left or right) is equal to k − 1 C n − 1 .
Thus, the 2 0 1 3 t h number on the 2 0 1 5 t h row is ( 2 0 1 5 − 1 ) C ( 2 0 1 3 − 1 ) = 2 0 1 2 ! 2 ! 2 0 1 4 ! = 2 2 0 1 4 × 2 0 1 3 = 2 0 2 7 0 9 1
The 2013th number on the 2015th row of Pascal's triangle is equal to the
coefficient of the 2013th term in the expansion of ( x + y )^2014 =
(2014 C 2012)/2 = 2027091
C stands for combination
Remember that triangular numbers are the numbers that are in the 3rd row.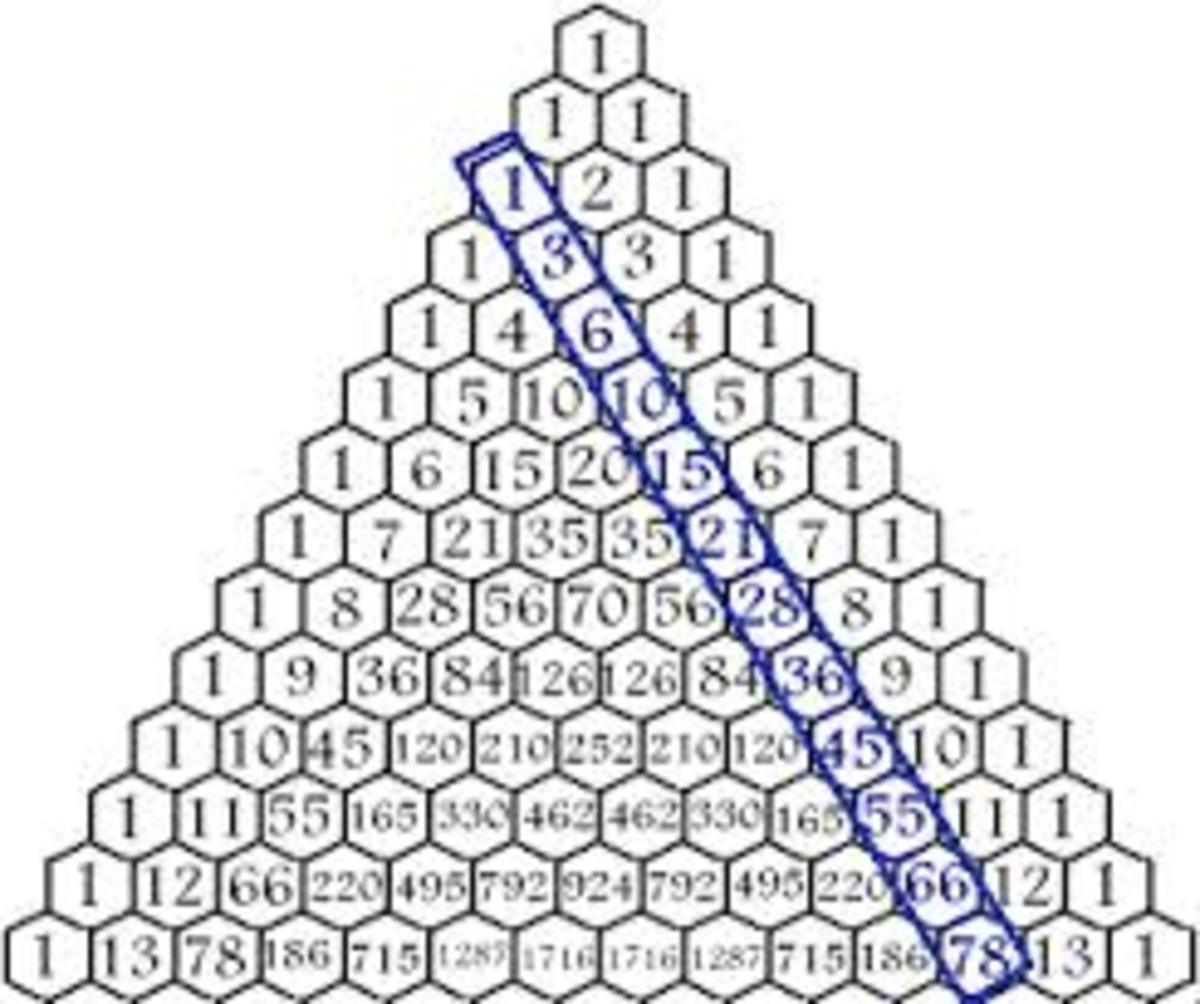
Just solve for the 2013th triangular number.
For the nth triangular number, the formula is (n^2+n)/2. Plugging in 2013 will get 2027091.
Another(almost identical) method is to look for the hexagonal numbers. Hexagonal numbers are every other triangular numbers, so you will be looking for the 1007th hexagonal number.
For the nth hexagonal number, the formula is 2n^2-n. Plugging in 1007 will also get 2027091.