Triangular Pyramids
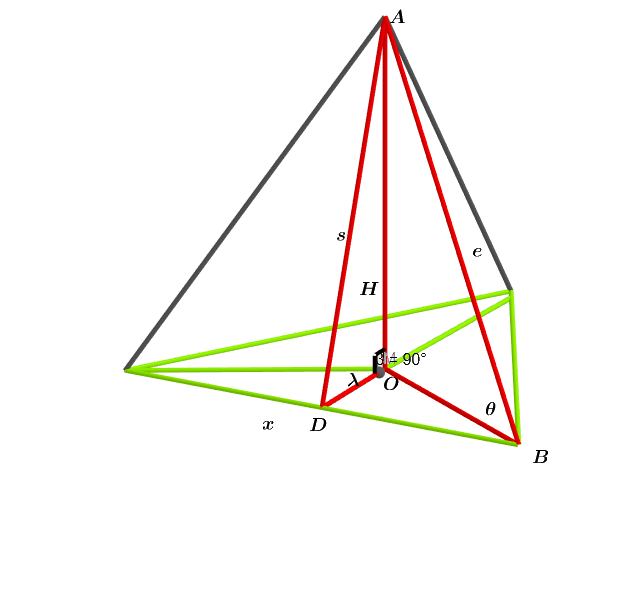
In the triangular pyramid above the lateral faces are isosceles triangles, , , and is the slant height and edge of the triangular pyramid, and is the height of the triangular pyramid and the base is an equilateral triangle.
Find the angle in degrees that minimizes the lateral surface area of the triangular pyramid when the volume is held constant, and find the angle in degrees.
Express the answer as in degrees.
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
V T = 4 3 1 x 2 H = K ⟹ H = x 2 4 3 K
Since the base is an equilateral triangle O B = 3 x and O D = 2 3 x .
H = x 2 4 3 K and O D = 2 3 x ⟹ The lateral surface area is A S = 2 3 x s = 4 x 3 x 6 + 5 7 6 K 2 ⟹ d x d A s = 4 3 ( x 2 x 6 + 5 7 6 K 2 2 x 6 − 5 7 6 K 2 ) ⟹ x = ( 1 2 ) 3 1 ( K ) 3 1 2 6 1 for x > 0 ⟹ H = 1 2 3 2 2 3 1 4 ∗ 3 2 1 K 3 1 ⟹
tan ( θ ) = x 3 H = 2 1 and tan ( λ ) = x 2 3 H = 2 and tan ( 9 0 − θ ) = cot ( θ ) = tan ( θ ) 1 = 2 = tan ( λ )
∴ θ + λ = 9 0 ∘ .
Testing for a minimum at x = ( 1 2 ) 3 1 ( K ) 3 1 2 6 1 :
For x = 0 . Since the denominator of d x d A s is always positive we just need to test the numerator.
For 0 < x < ( 1 2 ) 3 1 ( K ) 3 1 2 6 1 pick x = ( 1 2 ) 3 1 ( K ) 3 1 ⟹ d x d A s < 0
For x > ( 1 2 ) 3 1 ( K ) 3 1 2 6 1 pick x = 2 ∗ ( 1 2 ) 3 1 ( K ) 3 1 ⟹ d x d A s > 0
⟹ minimum at x = ( 1 2 ) 3 1 ( K ) 3 1 2 6 1 .