Triangular spider web

My solution is based on minimising the total energy stored in the elastic threads. The energy is proportional to the square of the extension, and we take the extensions to be equal to the lengths shown in the problem.

Construct a coordinate axes with the origin at A and let the point where the three strands join be (x,y). Then use Pythagoras Theorem to find the squares of the lengths to see that the energy is proportional to

$x^2+y^2+(90-y)^2+(30-x)^2+(60-x)^2+(30-y)^2=3(x^2+y^2-60 x -80 y) +\text{constant}$

Completing the squares lets us write this as

$3(x-30)^2+3(y-40)^2+\text{a different constant}$

Since the first two terms can never be negative, the energy is minimised when they are both zero, in other words when x = 30 and y = 40. Using Pythagoras one more time then gives us the required length as $\boxed{50}$

The tension force $\vec F_i$ along the thread $i$ corresponds (except for a prefactor $-k$ ) to the connecting vector between the points $i$ and $D$ : $\vec F_i = - k \left( \vec r_i - \vec r_D \right), \quad i = A, B, C$ The position vectors are given by $\vec r_A = \left( \begin{array}{c} 0 \\ 0 \end{array} \right), \quad \vec r_B = \left( \begin{array}{c} 60 \\ 30 \end{array} \right), \quad \vec r_C = \left( \begin{array}{c} 30 \\ 90 \end{array} \right), \quad \vec r_D = \left( \begin{array}{c} x \\ y \end{array} \right)$ In equilibrium, the sum of all forces must be zero: $\begin{aligned} & & 0 &\stackrel{!}{=} \sum_{i = A, B, C} \vec F_i \\ & & &= - k \left( \sum_{i = A, B, C} \vec r_i - 3 \vec r_D \right) \\ \Rightarrow & & \vec r_D &= \frac{1}{3} \sum_{i = A, B, C} \vec r_i \\ & & &= \left( \begin{array}{c} 30 \\ 40 \end{array} \right) \\ \Rightarrow & & l_A &= |\vec r_D| \\ & & &= \sqrt{30^2 + 40^2} \\ & & &= 50 \end{aligned}$ Thus, the point $D$ corresponds to the center of gravity of the triangle $ABC$ .

Let us resolve the tensions in the three threads into the $x$ and $y$ components parallel to the frame sides. Since the tension is directly proportional to the length of the thread $l_i$ so are the $x$ and $y$ components of the tension to the $x$ and $y$ lengths.

Equating the two components of tension we have $\begin{cases} \color{#3D99F6} x_A = x_B+x_C & ...(1) \\ \color{#D61F06} y_A+y_B = y_C & ...(2) \end{cases}$

We also note that $\begin{cases} x_A+x_B = 60 & ...(3) \\ x_A + x_C = 30 &...(4) \end{cases}$

$\begin{aligned} (3)+(4): \quad 2x_A + \color{#3D99F6} x_B + x_C & = 90 & \small \color{#3D99F6} (1): \ \ x_A = x_B+x_C \\ 3x_A & = 90 \\ \implies x_A & = 30 \end{aligned}$

Similarly, $\begin{cases} y_A - y_B = 30 & ...(5) \\ y_A + y_C = 90 & ...(6) \end{cases}$

$\begin{aligned} (5)+(6): \quad 2y_A \color{#D61F06} - y_B + y_C & = 120 & \small \color{#D61F06} (2): \ \ y_A+y_B = y_C \implies y_A = - y_B + y_C \\ 3y_A & = 120 \\ \implies y_A & = 40 \end{aligned}$

Therefore, $I_A = \sqrt{x_A^2 + y_A^2} = \sqrt{30^2+40^2} = \boxed{50}$ .

Suppose there were two threads instead of three. The point D would, of course, be halfway between them.

Now suppose one of those threads were a double thread. Think of A and B at the same place and C on the other side. D would then be closer to A. In fact, DA:DC = 1:2. It reminds me of the law of the lever.

Next, imagine A and C as they are in the picture buy B at (60,0). D would clearly be at (30,30). This point is the Centroid of the triangle ABC, the balancing point.

So all we need to do is average the x and y coordinates to find D. $D_{x}=\frac{0+60+30}{3}=30$ , $D_{y}=\frac{0+30+90}{3}=40$ . Then apply the distance formula from $(0,0)$ to $(30,40)$ which gives $\boxed{50}$

A geometrical solution:

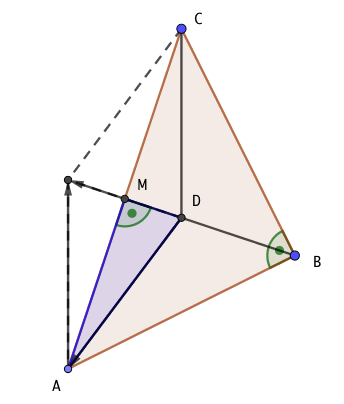
ABC is an isosceles rectangular triangle ( $\overline{AB}= \overline{BC} = 30 \cdot \sqrt{5}$ and $\overline{AC} = 30 \cdot \sqrt{10}$ ).

Since all three threads are physically the same it is a symmetrical problem and the point D has to be on the axis of symmetry, the median.

The vectors $\vec{DA}, \vec{DB}$ and $\vec{DC}$ are proportional to the tension forces, therefore the sum of $\vec{DA}$ and $\vec{DC}$ must equal $-\vec{DB}$ .

Let M be the midpoint of $\overline{AC}$ , then $\vec{DM} = \frac{1}{2} \cdot ( \vec{DA} + \vec{DC}) = -\frac{1}{2} \cdot \vec{DB}$ .

Because of $\overline{BM} = \overline{AM} = \frac{1}{2} \cdot 30 \cdot \sqrt{10}$ consequently follows $\overline{DM} = \frac{1}{3} \cdot \overline{BM} = \frac{1}{3} \cdot \frac{1}{2} \cdot 30 \cdot \sqrt{10} =5 \cdot \sqrt{10}$ .

$l_A = \overline{DA}$ is the hypotenuse of the rectangular triangle ADM, wich can be calculated by the Pythagoras theorem: $l_A=\sqrt{ \overline{AM}^2 + \overline{DM}^2} = \sqrt{(15 \cdot \sqrt{10})^2 + 5 \cdot \sqrt{10})^2} = \boxed{50}$ .

Let $z_1,z_2,z_3$ be the complex numbers which represent the line $l_A,l_B,l_C$ and the direction of them are all pointing to the center.

Because the equilibrium state, the force vector must sum to zero, but the assumption $F=-kl_i$ state that the lines aka the complex number will also sum to zero. Let's start:

By letting $z_k=a_k+b_ki$ for $k=1,2,3$ , we have below six-equation group: $\begin{cases}a_1-a_2=60\\a_1-a_3=30\\b_1-b_2=30\\b_1-b_3=90\\a_1+a_2+a_3=0\\b_1+b_2+b_3=0\end{cases}$

Summing up the first, second and the fifth equation gets us $a_1=30$ .

Summing up the third, fourth and the fifth equation gets us $b_1=40$ .

So $|z_1|=\sqrt{30^2+40^2}=\boxed{50}$ .

Think of a,b,c as the vectors AD,DB and DC respectively.

So a+b = AB = (60,30) and a+c = AC = (30,90)

Adding these together gives

2a + (b+c) = (90,120)

Since the forces at D are in equilibrium and they are proportional to the length of the vectors we also have

-a + b + c = 0 => a = b + c

Substituting (b+c) in our earlier result gives

3a = (90,120) => a = (30,40)

=> length of a is 50.

Directly, measure the length of la on the monitor screen using a ruler. Use the 30 cm on the RHS to scale the measured length. Then, you will get 50 cm.

My hypothesis, unproven as of yet, is that the point D is at the centroid of triangle ABC. It helped in solving that the triangle ABC is isosceles, with side AB having the same length as side BC. The centroid is located a distance 2/3 of the way to the opposite side. Starting from B, the line that bisects side AC intersects it at right angles, allowing for use of the Pythagorean theorem to solve for the location of the centroid that presumably is also point D.