Triangular Thirds
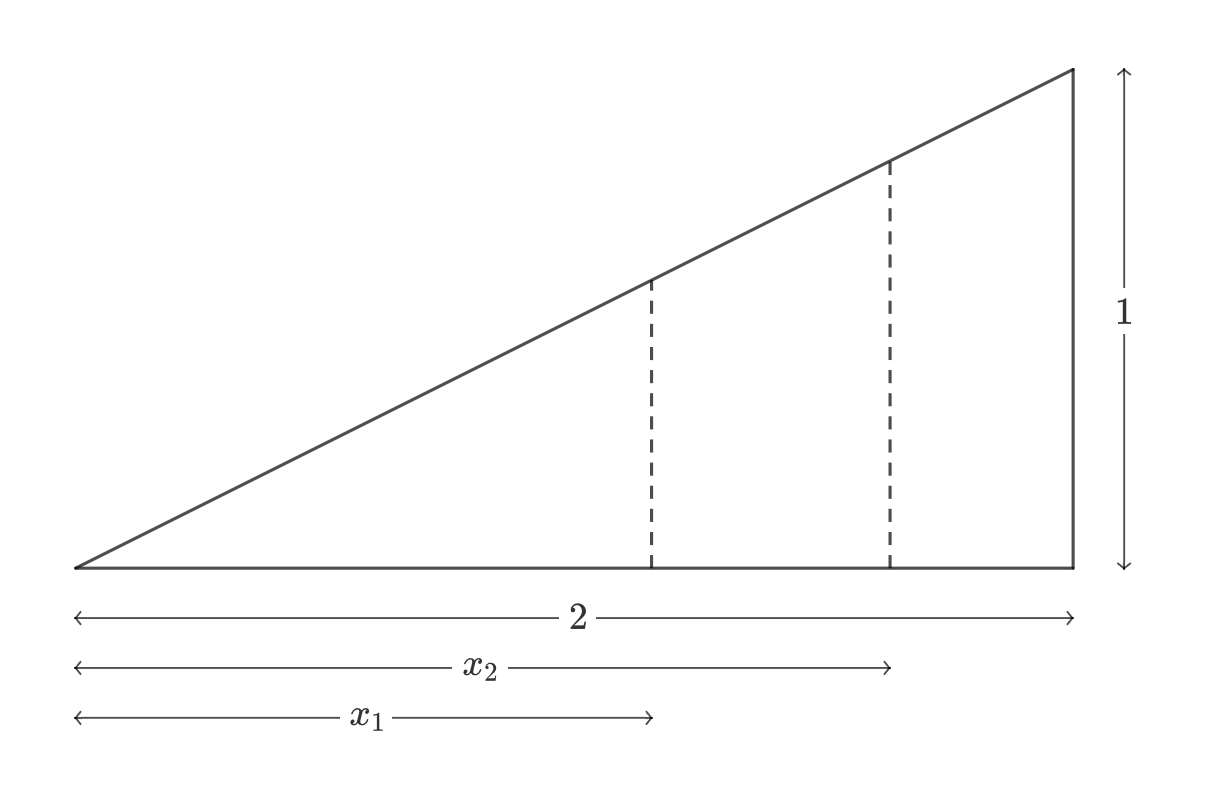
Two vertical lines lie x 1 and x 2 units along the base of a right-angled triangle, cutting it into 3 equal areas (See diagram above).
What is the value of x 1 x 2 ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
For figures of similar shape, in the case a right triangle with legs of 1 : 2 . the area of the figure is directly proportional to the square of the linear dimension. That is A ∝ x 2 ⟹ x 1 2 x 2 2 = A 1 A 2 = 2 ⟹ x 1 x 2 = 2 .
The triangle with base x 2 is similar to, and has twice the area of the triangle with base x 1 . The scale factor of the areas is the square of the scale factor of the sides for similar shapes; hence x 1 x 2 = 2 .
In fact, by comparing with the triangle of base 2 , we can work out explicitly that x 1 = 3 2 3 and x 2 = 3 2 6 .
The area of the whole triangle is 2 1 ⋅ 2 ⋅ 1 = 1 , so we expect each section to have an area of 3 1 . The leftmost section is a right-angled triangle similar to the large one, so it has a base of x 1 and a height of 2 1 x 1 . If we label the area of this section A 1 , we have: A 1 = 2 1 ⋅ x 1 ⋅ 2 1 x 1 ( 2 1 x 1 ) 2 2 1 x 1 x 1 = 3 1 = 3 1 = 3 1 = 3 2 The middle section is not a right-angled triangle, but its area can be expressed as A 2 = 2 1 ⋅ x 2 ⋅ 2 1 x 2 − A 1 , so we have: A 2 = 2 1 ⋅ x 2 ⋅ 2 1 x 2 − A 1 ( 2 1 x 2 ) 2 − 3 1 ( 2 1 x 2 ) 2 2 1 x 2 x 2 = 3 1 = 3 1 = 3 2 = 3 2 = 3 2 ⋅ 2 Thus, we have x 1 x 2 = 2