Triangular Tic-Tac-Toe

Logic Level 2

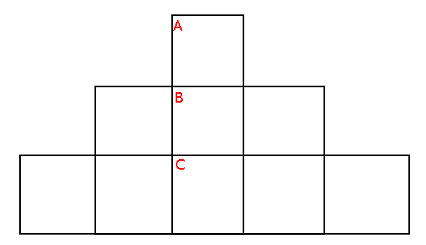
Alice and Bob are playing Tic-Tac-Toe on the above triangular board. They play as in in normal Tic-Tac-Toe: taking turns, each player claims one square. The first to claim three squares in a row (vertically, horizontally, or diagonally) wins.

Alice plays first. Alice and Bob both want to win and play optimally. Which of the following is true?

Alice's first move is in square A and Alice wins. Neither Alice nor Bob get three squares in a row. Alice's first move is in square B and Alice wins. Bob wins. Alice's first move is in square C and Alice wins.

Maggie Miller by Maggie Miller , 27, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Mikael Marcondes
Jul 17, 2015

Numbering each square as below, Alice can take an optimal strategy and win if she begins marking the box number 7 (i. e. C square).

Alice may play as follows:

S 1 = A : 7 , B : 1 , 2 , 3 , 4 , 5 ; A : 8 , and Alice wins on the next turn; S_1={A: 7, B: 1, 2, 3, 4, 5; A: 8, \text{ and Alice wins on the next turn;}}

S 2 = A : 7 , B : 9 ; A : 6 , and Alice wins on the next turn; S_2={A: 7, B: 9; A: 6, \text{ and Alice wins on the next turn;}}

S 3 = A : 7 , B : 6 ; A : 9 , B : 1 , 2 , 3 , 4 , 5 and Alice wins on the next turn; S_3={A: 7, B: 6; A: 9, B: 1, 2, 3, 4, 5 \text{ and Alice wins on the next turn;}}

S 4 = A : 7 , B : 6 ; A : 9 , B : 8 ; A : 1 and Alice wins on the next turn; S_4={A: 7, B: 6; A: 9, B: 8; A: 1 \text{ and Alice wins on the next turn;}}

S 5 = A : 7 , B : 8 ; A : 5 , B : 1 , 2 , 3 , 4 , 9 and Alice wins on the next turn; S_5={A: 7, B: 8; A: 5, B: 1, 2, 3, 4, 9 \text{ and Alice wins on the next turn;}}

S 5 = A : 7 , B : 8 ; A : 5 , B : 6 ; A : 1 and Alice wins on the next turn. S_5={A: 7, B: 8; A: 5, B: 6; A:1 \text{ and Alice wins on the next turn.}}

All possibilities are covered. Hence, if Alice starts and marks the C square, in a optimal stratregy, she wins.

6 Helpful 1 Interesting 2 Brilliant 0 Confused

@Maggie Miller , do you know if is there a formal way to present this result as logical consequences?

Mikael Marcondes - 5 years, 11 months ago

Log in to reply

Not as far as I know, but you can reduce the number of cases to check by symmetry (while remaining formal).

Assume Alice plays on 7. If Bob doesn't play on 8 or 9, then Alice will and then will win on the next move. If Bob plays on 8 or 9, assume without loss of generality (by symmetry) that he played on 8. Alice plays on 1, Bob is forced to play on 3, Alice plays on 5 and wins on her next turn.

Technically, you would also need to show that you KNOW Alice will play on square 7 - you've shown that she will win if she plays on square 7, but perhaps she could also guarantee a win by playing first on a different square (so could start with a different square while still playing optimally). The process for checking other squares is similar and not extremely pleasant, though.

Maggie Miller - 5 years, 11 months ago

Log in to reply

I've assumed she plays initially on seven because it's on the options, but I'd really like to know why I should begin thinking logically from this square and not another. Checking cases would be very cloying, though.

Mikael Marcondes - 5 years, 11 months ago

But it's not necessarily guaranteed that she will win, just puts the game in her favor. For example, if Bob follows her mark of the 7 with a mark of the 8 square, she would go to the 6 (or the 3, doesn't matter). Bob would block and then take the five after.

Tim Stewart - 5 years, 6 months ago

Log in to reply

That's the point. Alice plays optimally. If Bob follows her mark of the 7 with a mark of the 8, she would go not for 6 (or 3), but for 5 (or 1), threatening to win the game on the next turn with 6 (or 3). Bob fills the square which would give the victory to Alice, and she goes to the other unfilled (e. g., if she had marked 5, now she marks 1, and vice-versa). As you can follow the turns of each one, now she has a diagonal and a column (or a row, depending on the way her turns succeed) and wins.

Mikael Marcondes - 5 years, 6 months ago

What about S3 if B plays 8: 7,6,9,8

Matthew Li - 5 years, 1 month ago

Log in to reply

Alice can then play 1. Bob can try to block in 3 or 4, and Alice will win by playing in 3 or 4 according to whichever one Bob left open.

Adam Davis - 4 years, 9 months ago

think simply this way, if Alice's first move in square C then Bob's must move beside horizontal of square C otherwise will be lose. then Alice's 2nd move is in square A. so Bob's move in square B. then if Alice move in down right corner or down left corner [depend on Bob's move] and win by Alice's next move.....

Naimur Nam - 4 years, 8 months ago
Saya Suka
Apr 14, 2021

C is part of 4 winning positions, the most out of all the 9 boxes. A has 3 and B only 2.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...