Triangulations

I use the following "strategy" to determine the largest equilateral triangle that can inscribe in a square. We know that the longest straight line we can draw in a square is the diagonal $AC$ (see diagram). If we use $AC$ as the base of the equilateral triangle and if it can inscribe in the square it is definitely the largest of such triangle, but it cannot as most of triangle is outside the square. If we reduce the length of the baseline (the line joining the left-bottom vertex of the square and the right vertical side $AC'$ ) to be shorter than the diagonal. We note that $\angle \theta$ reduces from $45^\circ$ and more of the triangle is within the square. Since when $\theta=0^\circ$ , the entire triangle is inscribed the square with its top vertex a distance away from the top side of the square. This means at a certain $\theta$ , the entire triangle is inscribed in the square with it top vertex touching the top side of the square. This is the largest triangle we are looking for.

Now let the side length of square $ABCD$ be 1. The midpoints of $AD$ , $AC'$ , and $BC$ be $F$ , $G$ , and $H$ . Then the side length of the equilateral triangle $AC'=C'E=AE=\sec \theta$ . The altitude of triangle $EG = \frac {\sqrt 3}2 \sec \theta$ . Since $\angle EGH = \theta$ , $HG = EG \cos \theta = \frac {\sqrt 3} 2$ , Also $\triangle AC'D$ and $\triangle AGF$ are similar. Therefore $\frac {GF}{C'D} = \frac {AF}{AD} = \frac 12$ $\implies GF = \frac 12 C'D = \frac 12 \tan \theta$ .

Now note that

$\begin{aligned} HG + GF & = 1 \\ \frac {\sqrt 3}2 + \frac 12 \tan \theta & = 1 \\ \tan \theta & = 2 - \sqrt 3 \\ \implies \theta & = 15^\circ \end{aligned}$

Since $\boxed {15}^\circ$ is the smallest angle a side of the triangle makes with a side of the square it is the answer required.

Using the origin as the point around which to rotate the triangle and realizing that the answer had to be symmetrical around the y=x line, the answer had to be $\frac{90^o-60^o}{2} \Longrightarrow 15^o$ . I used Wolfram Mathematica 11.3 and a Manipulate command to visualize the situation using a triangle base reaching from the origin to the far vertical size of the square.

Comrade Chew-Seong Cheong has posted a fine solution. For the sake of variety, let me share my own solution.

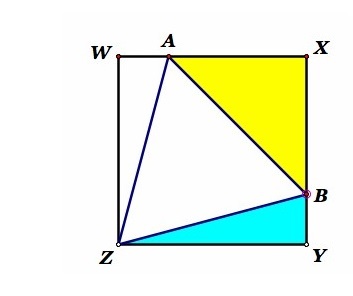
Consider an equilateral triangle residing inside a square $XYZW$ . We can shift the triangle horizontally or vertically so that one of its vertices coincides with a vertex of the square, say, $Z$ . Thus, without loss of generality, we can restrict our inquiry to an equilateral triangle with $Z$ as one of its vertices.

Among these triangles, let's first study the one whose other vertices $A$ and $B$ are located on sides of the square, as shown in the figure. The triangles $\Delta ZWA$ and $\Delta ZYB$ will be congruent, so that $\angle WZA = \angle YZB = \frac{90-60}{2}=15$ degrees.

We claim that the area of any other equilateral triangle $\Delta ZA'B'$ (with $\angle A'ZY > \angle B'ZY$ ) is less than the area of $\Delta ZAB$ . Indeed, if $\angle B'ZY<15$ degrees, then $ZB'$ is shorter than $ZB$ , by Pythagoras, and if $\angle B'ZY> 15$ degrees, then $\angle WZA'<15$ degrees, and $ZA'$ will be shorter than $ZA$ .

Thus the answer is $\boxed{15}$ degrees.