Triangulo loco
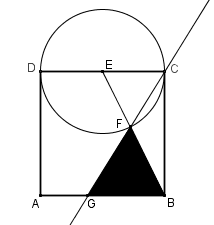
Let A B C D be a square of side length 2, E is the midpoint of D C , E C is the radius of the circle. The circle cuts E B in F and the extension of F C cuts A B in G .
Find the area of △ F G B .
If the area can be written as d a b − c , where a and c are positive integer, with b and d are primes . Submit your answer as a + b + c + d .
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
Good solution hunting down the lengths and angles of the triangle.
Nice solution! Is there a solution without use trigo?
Log in to reply
I suspect there is a solution using similarity of △ B F G and △ E C F or △ B G C and △ D C F .
Log in to reply
I noticed your comment after I posted my solution, so I think we're on the same wavelength. :)
In rt. triangle CEB, ED= 5 and SinCEB= 5 2 .
Area of isosceles triangle CEF= 2 1 ∗ S i n C E B ∗ 1 2 = 5 1 .
Since GB | | CE, triangles GBF and CEF are similar and FB:EF::( 5 -1):1.
S o a r e a Δ F G B = a r e a Δ C E F ∗ ( E F F B ) 2 = 5 1 ∗ ( 5 − 1 ) 2 . = 5 6 − 2 ∗ 5 = 5 6 5 − 1 0 = d a b − c . a + b + c + d = 6 + 5 + 1 0 + 5 = 2 6 .
Let the perpendicular from F to C D intersect this side at P . Then Δ E F P is similar to Δ E B C , and so
∣ E F ∣ ∣ F P ∣ = ∣ E B ∣ ∣ B C ∣ ⟹ ∣ F P ∣ = 5 2 , since ∣ E F ∣ = 1 and ∣ E B ∣ 2 = ∣ E C ∣ 2 + ∣ C B ∣ 2 .
The area of Δ F C E is then 2 1 ∣ E C ∣ ∣ F P ∣ = 2 1 × 1 × 5 2 = 5 1 .
Now note that triangles Δ F C E and Δ F G B are similar. Letting Q be the point on A B where the perpendicular from F intersects that side, we have that
∣ F P ∣ ∣ F Q ∣ = ∣ F P ∣ 2 − ∣ F P ∣ = 5 2 2 − 5 2 = 5 − 1 ,
and thus the area of Δ F G B will be ( 5 − 1 ) 2 that of Δ F C E , since by similarity we will have ∣ G B ∣ = ( 5 − 1 ) ∣ C E ∣ as well. Thus the desired area will be
( 5 − 1 ) 2 × 5 1 = 5 6 − 2 5 = 5 6 5 − 1 0 .
This results in a final answer of a + b + c + d = 6 + 5 + 1 0 + 5 = 2 6 .
Nice solution. You can also say point P is just point D by the converse of Thales' Theorem.
ΔFGB is similar to ΔEFC. By trigonometry,sin <CEF =2/√5, The area [EFC] = 1/√5, The area ratio is the square of length ratio,
(1/√5)/[FBG] =(〖1/(√5-1))〗^2, So the area of triangle FBG,
[FBG] = (6√5-10)/5 , a+b+c+d = 26
Let ∠ B E C = α :
sin ( α ) = 5 2
∠ F B G = 9 0 ∘ − ∠ E B C = 9 0 ∘ − ( 9 0 ∘ − α ) = α
E F = F C ⇒ ∠ E F C = ∠ G F B = 9 0 ∘ − 2 α
∠ F G B = 1 8 0 ∘ − ∠ F B G − ∠ F G B = 9 0 ∘ − 2 α = ∠ G F B ⇒ F B = B G
E F = E C = 1 , E B = 1 2 + 2 2 = 5 ⇒ F B = B G = E B − E F = 5 − 1
Δ ( F B G ) = 2 1 × sin ( α ) × F B × B G = 2 1 × 5 2 × ( 5 − 1 ) 2
⋯ = 5 5 × ( 6 − 2 5 ) = 5 6 5 − 1 0
a = 6 , b = 5 , c = 1 0 , d = 5 ⇒ a + b + c + d = 2 6