Trick or treat!

The trick is to create a segment $\overline{BF}$ in such a way the angle B is divided in two parts equals to $20°$ . The rest is all about finding the isosceles triangles.

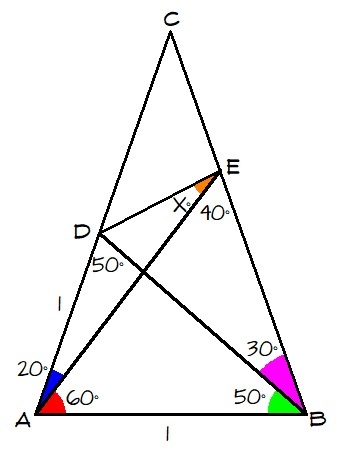Consider the diagram.

$\angle BDA=180-20-60-50=50$

$\angle AEB=180-60-30-50=40$

Since $\angle ADB=\angle DBA=50$ , $\triangle ADB$ is isosceles with $AD=AB$ .

Let $AD=AB=1$ .

Apply sine law on $\triangle AEB$ .

$\dfrac{AE}{\sin 80}=\dfrac{1}{\sin 40}$ $\implies$ $AE \approx 1.532$

Appy cosine law on $\triangle ADE$ .

$(DE)^2=1^2+1.532^2-2(1)(1.532)(\cos 20)$ $\implies$ $DE \approx 0.684$

Apply sine law on $\triangle ADE$ .

$\dfrac{\sin x}{1}=\dfrac{\sin 20}{0.684}$

$x=\sin^{-1}0.5=30^\circ$

$3x-1=3(30)-1=$ $\boxed{89}$

I had solved similar problems with different symbols for some points as follows:

$\text{From the given angles we can easily get value of following angles.}\\ BCD=80, ~~CDB=40, ~~CEB=50, ~~DOC=110,~external~ angle~ of~ \Delta ~DEO, \\ EDB=n, ~~\therefore DCE=110-n. ~and ~\color{#3D99F6}{\angle DEB=50+110+n=160+n} ~~ \text{Let x=BC, and y=BD}.\\ \angle CEB=50=BCE,~~\therefore~~x=BC=BE.\\ Applying ~Sine ~ Law ~\dfrac {SinP}{SinQ}=\dfrac p q~to~\Delta s ~EBD ~and ~DBC, \\ \dfrac {Sin(n)}{Sin(160 - n)}=\dfrac x y=\dfrac {Sin(40)}{Sin(80)}, ~expanding ~ Sin(160 - n),\\ and ~dividing~ by~ Sin(n), ~,~~~\dfrac 1 {Sin160*Cot(n) - Cos160}=\dfrac {Sin(40)}{Sin(80)}\\ Soving ~n=30, 3*n - 1=\Large ~~~~\color{#D61F06}{89}$

Being a fan of Algebra I went through the process of perceiving the triangle as a highways of lines on an x-y grid, then isolating the points E, D and F (the crossing of lines BD and EC) to create the angle CDE giving me a definite value of n. I chose to put a length of 10 to the line BC as the size of the triangle would impact the co-ordinates, but not the angles.

Typed solution: If AB=AC then angle ABC=angle ACB=80

tan(60)=rt(3) so line BD can be expressed as y=rt(3)x tan(80)=5.67 so line BA can be expressed as y=5.67x but also AC can be expressed as y=56.7 - 5.67x tan(50)=1.19 so line EC can be expressed as y=11.9 - 1.19x

Point E lies on the point when lines BA and EC meet so BA=EC implies that: 5.67x=11.9 - 1.19x so x=1.7 as x=1.7 BA would read y=5.67(1.7)=9.84 so E=(1.7 , 9.84)

Point F lies on the point when lines EC and BD meet so BD=EC implies that: rt(3)x=11.9 - 1.19x so x=4.07 as x=4.07 BD would read y=rt(3)(4.07)=7.06 so F=(4.07 , 7.06)

Point D lies on the point when lines AC and BD meet so BD=AC implies that: rt(3)x=56.7 - 5.67x so x=7.6 as x=7.6 BD would read y=rt(3)(7.6)=13.2 so D=(7.6 , 13.2)

Now having my co-ordinates i can assess the angles that would amount up to the angle FED by first finding the angle above the y co-ordinate of E, then below the y-co-ordinate of E.

Theta =tan^-1((13.2-9.84)/(7.6-1.7)) =30 Alpha =tan^-1((9.84-7.06)/(4.07-1.7))=50

Now, since angle BFC is created by two lines, then angle EFD has to be symmetrical to it, so EFD=70

Finally finishing as Theta, Alpha, EFD and n have to add up to 180 we get n=30.

Since the question asked for 3n-1 the answer is 89