A geometry problem by Toto Mub
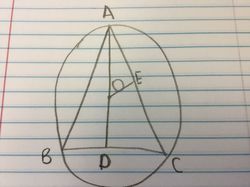 Triangle ABC is inscribed in circle O
Triangle ABC is inscribed in circle O
Line segment OE bisects line segment AC.
Line segment OD = 1
Line segment AC = 12
Figure out the radius of circle O
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
So, we know that AC is 12.
Write then, OD as 1.
So AD is r+1, since AO is the radius.
We can up the Pythagorean theorm to prove that ( r + 1 ) 2 + ( D C ) 2 = 1 4 4
Then, we draw a line from O to C making line OC, which is also the radius.
We have another right triangle, and so we use the theorm again.
Giving 1 + ( D C ) 2 = r 2
We now know that D C 2 = r 2 + 1
If we plug that in to the other triangle, then 2 r 2 + 2 r = 1 4 4
We can divide each side by 2, giving r 2 + r = 7 2
That makes ( r + 9 ) ( r − 8 ) = 0
So r = -9 or 8. But we can't have a negative radius, so the answer is 8.
Let AO = x, OC = x, OD = 1, DC = y. Then (x + 1)^2 + y^2 = 144 and y^2 + 1 = x^2. Substituting, x^2 + x - 72 = 0 = (x + 9)(x - 8), so x = 8. Ed Gray