Tricky altitudes

An easy geometrical solution

Let $AC=BC=x$

Using $r=\frac { \Delta }{ s }$ and $R=\frac { abc }{ 4\Delta }$ , where $s=\frac { a+b+c }{ 2 }$ and ${ \Delta }^{ 2 }=s(s-a)(s-b)(s-c)=\frac { s(b+c-a)(a+c-b)(a+b-c) }{ 8 }$

Now since

$\frac { r }{ R } =\frac { 3 }{ 8 }$

$\Leftrightarrow \frac { 4{ \Delta }^{ 2 } }{ sabc } =\frac { 3 }{ 8 }$

$\Leftrightarrow \frac { (b+c-a)(a+c-b)(a+b-c) }{ abc } =\frac { 3 }{ 4 }$

$\Leftrightarrow \frac { (2x-2)(2)(2) }{ 2{ x }^{ 2 } } =\frac { 3 }{ 4 }$

$\Leftrightarrow 16(x-1)=3{ x }^{ 2 }$

$\Leftrightarrow 3{ x }^{ 2 }-16x+16=0$

$\Leftrightarrow (3x-4)(x-4)=0$

$\Leftrightarrow x=\frac { 3 }{ 4 } \vee x=4$

From Apollonius Theorem,

${ AC }^{ 2 }+{ BC }^{ 2 }=2({ CD }^{ 2 }+{ AD }^{ 2 })$

$\Leftrightarrow 2x^{ 2 }=2({ CD }^{ 2 }+1)$

$\Leftrightarrow { CD }^{ 2 }={ x }^{ 2 }-1$

$\Leftrightarrow { CD }^{ 2 }=15\vee \frac { 7 }{ 9 }$

$\therefore a=15\quad and\quad \frac { m }{ n } =\frac { 7 }{ 9 }$

$\Rightarrow a+m+n=31$

An analytical approach

Choose a Cartesian coordinate system with D as it's origin, points A and B on the x -axis such that $A(-1,0)$ and $B(1,0)$ . Point C is on the y -axis such that $C(0,c)$ . G is the center of the inscribed circle, F is the center of the circumscribed circle and E is the midpoint of BC .

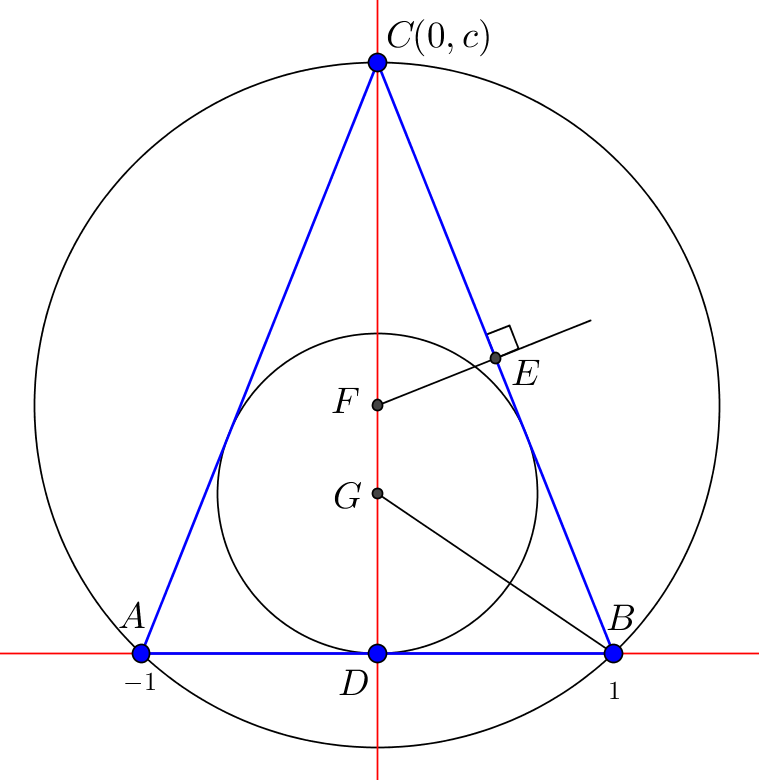
A vector equation of $EF$ is $EF: \binom{\frac{1}{2}}{\frac{1}{2}c} + \lambda \cdot \binom{c}{1}$

The x -coordinate of F is 0, so: $\frac{1}{2} + \lambda \cdot c = 0 \Rightarrow \lambda = -\frac{1}{2c}$

It follows that: $F = \big(0 , \frac{1}{2}c - \frac{1}{2c}\big) = \big(0 , \frac{c^2-1}{2c}\big)$

and: $CF = c - \frac{c^2-1}{2c} = \frac{c^2+1}{2c}$

Let $DG = h$ , so $G(0,h)$ , then the distance from G to BC is: $d(G, BC) = \frac{\mid h-c \mid}{\sqrt{c^2+1}}$

This results in: $h = \frac{\mid h-c \mid}{\sqrt{c^2+1}} \Rightarrow DG = h = \frac{-1 + \sqrt{c^2+1}}{c} \quad (\text{because} \; h < c)$

We know that the ratio of the radii $r_1 : r_2 = 3 : 8$ , so $8 \cdot DG = 3 \cdot CF$ or $8h = 3 \cdot CF$ , so:

$\begin{aligned} & \quad \frac{-8+8\sqrt{c^2+1}}{c} = 3 \cdot \frac{c^2+1}{2c} \\ \Leftrightarrow & \quad -16 + 16\sqrt{c^2+1} = 3c^2+3 \\ \Leftrightarrow & \quad 16\sqrt{c^2+1} = 3c^2+19 \\ \Leftrightarrow & \quad 9c^4 - 142c^2 + 105 = 0 \\ \Leftrightarrow & \quad 9(c^2)^2 - 142c^2 + 105 = 0 \\ \Leftrightarrow & \quad (9c^2 - 7)(c^2 - 15) = 0 \\ \Leftrightarrow & \quad c^2 = \frac{7}{9} \vee c^2 = 15 \end{aligned}$

Because $CD = c$ the values we're interested in are $a = 15$ and $\frac{m}{n} = \frac{7}{9}$ and therefore the desired sum is: $a + m + n = 15 + 7 + 9 = 31$

A solution without much calculation:

Let $R, r$ be the circumradius, inradius of $\triangle ABC$ respectively. We know that $FG^2=R(R-2r)$ . Letting $r=3x$ and $R=8x$ , we see $FG^2=8x(8x-6x)=16x^2\implies FG=4x$ . Therefore, $FD = FG \pm r = 4x\pm 3x = 7x\text{ or } x$ depending on which side $D$ is on.

We know that $AD=\dfrac{1}{2}AB=1$ .

If $D$ is closer to $G$ than $F$ , then by Pythagorean Theorem on $\triangle FAD$ , $1=AD^2 =FA^2-FD^2 =(8x)^2-(7x)^2=15x^2\implies x^2=\dfrac{1}{15}$ In this case $CD^2 = (R+FD)^2=225x^2 = \boxed{15}$ .

If $D$ is closer to $F$ than $G$ , then by Pythagorean Theorem on $\triangle FAD$ , $1=AD^2 =FA^2-FD^2 =(8x)^2-x^2=63x^2\implies x^2=\dfrac{1}{63}$ In this case $CD^2 = (R-FD)^2=49x^2 = \boxed{\dfrac{7}{9}}$ .

So $a=15$ , $m=7$ and $n=9$ which gives our final answer of $15+7+9=\boxed{31}$ .

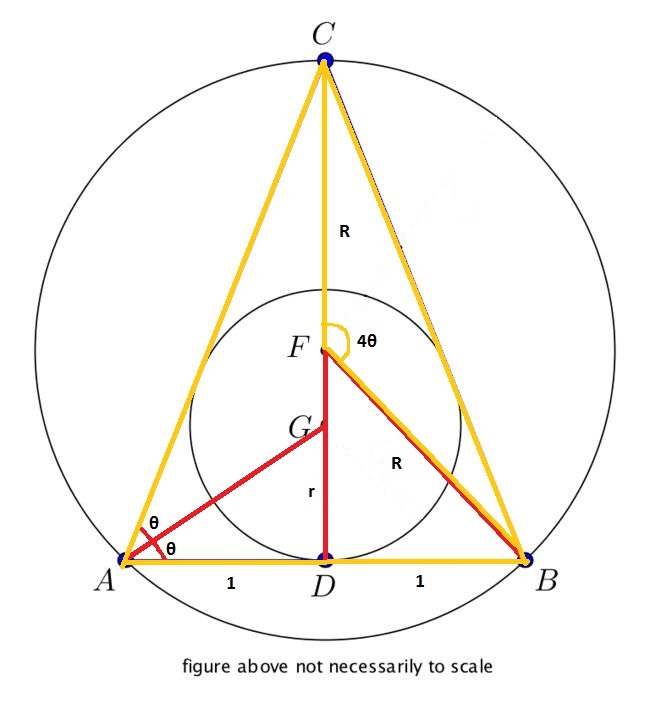
From the diagram, we can see that $tan \theta = r$ and $tan 2 \theta = CD$ . We can also find out that $sin 4 \theta = \frac {1}{R}$ . Since we know that $R = \frac {8}{3} r$ , we can then substitute $r = tan \theta$ into $sin 4 \theta = \frac {3}{8r}$ . Thus, we get $sin 4 \theta = \frac {3}{8 tan \theta}$ . Expand $sin 4 \theta$ into the form $4 sin \theta cos \theta (1 - 2sin^2 \theta)$ and $tan \theta$ to $\frac {sin \theta}{cos \theta}$ . Put them back into the equation and $cos \theta$ will cancel out nicely leaving a quadratic equation in terms of $sin^2 \theta$ which is $4 sin^2 \theta (1-2sin^2 \theta) = \frac {3}{8}$ . Solve the equation and obtain the two values of $\theta$ . Then, put them back into the equation $CD = tan 2 \theta$ and square it and you will get $\frac {7}{9}$ and $15$ .

Denote the area by $K$ .

$AC = BC = a , AB = 2 \implies s = a + 1$ . By Heron's Formula, we have $K = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{a^2-1}$ Thus, we have $\begin{aligned} rs & = \sqrt{a^2 - 1} \implies r = \frac{\sqrt{a^2 - 1}}{a+1} \\ \frac{abc}{4R} & = \sqrt{a^2 - 1} \implies R = \frac{a^2}{2\sqrt{a^2-1}} \end{aligned}$

Since $\frac{R}{r} = \frac{8}{3}$ , we have $\frac{R}{r} = \frac{\frac{a^2}{2\sqrt{a^2-1}}}{\frac{\sqrt{a^2-1}}{a+1}} = \frac{8}{3} \implies 3a^2 - 16a + 16 = 0 \implies a = \frac{4}{3}, 4$

Observe that the desired value is $a^2 - 1$ . The answer follows from substituting $a$ in.

Sorry, but I'm still learning LaTeX.

I solved the same way as Daniel Liu.

My solution is identical to the Daniel Liu