Tricky Area II
β α π 2 ( 4 1 ! ) 2
If the area bounded by the curve y = x 2 + x 2 + x 2 + ⋱ 1 1 1 and the x -axis is given above, where α and β are positive coprime integers, find α + β .
Try another similar problem: Tricky Area
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Rewriting the function as
y
=
x
2
+
y
1
And seeing the area,
A
as
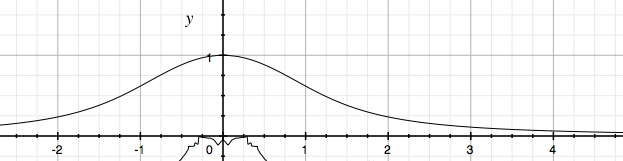
The function can be written in terms of x and then integrated from 0 to 1 just as a form of the beta function.
x = y 1 − y = y 1 − y 2
A = 2 ∫ 0 1 y 1 − y 2 d y Note: β ( a , b ) = 2 ∫ 0 1 x 2 a − 1 ( 1 − x 2 ) b − 1 d x
A = β ( 4 1 , 2 3 ) = 3 1 6 π 2 Γ ( 4 5 ) 2
Consider y as follows:
y y y 2 + x 2 y − 1 ⟹ y = x 2 + x 2 + x 2 + ⋱ 1 1 1 = x 2 + y 1 = 0 = 2 x 4 + 4 − x 2 Solving the quadratic equation for y
We note that y is even as shown in the figure. Now again consider:
y = x 2 + y 1 ⟹ x 2 = y 1 − y ⟹ x = y 1 − y
The area under the curve is given by A = ∫ − ∞ ∞ y d x = 2 ∫ 0 ∞ y d x = 2 ∫ 0 1 x d y . Therefore,
A = 2 ∫ 0 1 y 1 − y d y = 2 ∫ 0 1 y 1 − y 2 d y = 2 ∫ 0 1 y − 2 1 ( 1 − y 2 ) 2 1 d y = B ( 4 1 , 2 3 ) = Γ ( 4 7 ) Γ ( 4 1 ) Γ ( 2 3 ) = π Γ ( 2 7 ) 4 2 Γ ( 4 9 ) Γ ( 4 1 ) Γ ( 2 3 ) = π ⋅ 2 5 ⋅ 2 3 Γ ( 2 3 ) 4 2 ⋅ 4 5 Γ ( 4 5 ) ⋅ 4 Γ ( 4 5 ) Γ ( 2 3 ) = 3 1 6 π 2 Γ ( 4 5 ) 2 = 3 1 6 π 2 ( 4 1 ! ) 2 Note that beta function B ( m , n ) = 2 ∫ 0 1 x 2 m − 1 ( 1 − x 2 ) n − 1 d x where Γ ( s ) is gamma function. Using Γ ( 2 z ) = π 2 2 z − 1 Γ ( z ) Γ ( z + 2 1 ) Using Γ ( 1 + z ) = z Γ ( z ) Note that Γ ( 1 + z ) = z !
⟹ α + β = 1 6 + 3 = 1 9
References: