Tricky Area
The area bound by the two coordinate axes and is for integers , where is not the multiple of the cube of a prime.
Submit your answer as .
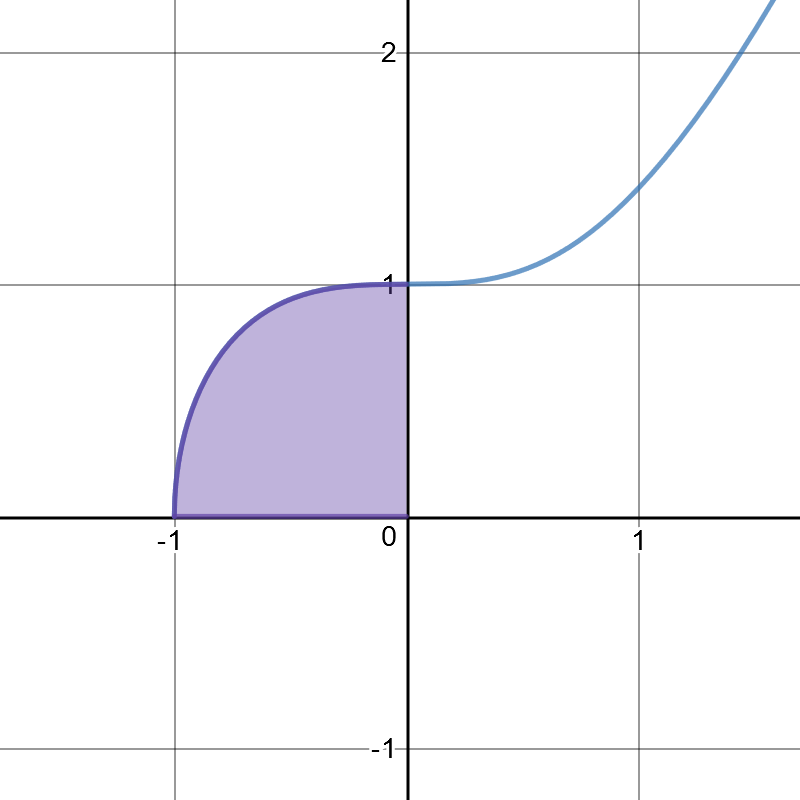
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Firstly, we use the substitution y = − x 3 to show that the area is equal to A = ∫ − 1 0 1 + x 3 d x = 3 1 ∫ 0 1 y − 3 2 ( 1 − y ) 2 1 d y = 3 1 B ( 3 1 , 2 3 ) = Γ ( 6 1 1 ) Γ ( 3 1 ) Γ ( 2 3 ) = 5 π Γ ( 6 5 ) Γ ( 3 1 ) using the identity Γ ( z + 1 ) = z Γ ( z ) a couple of times, and the fact that Γ ( 2 1 ) = π . The duplication formula 2 π Γ ( 2 z ) = 2 2 z − 2 1 Γ ( z ) Γ ( z + 2 1 ) gives us that A = 5 π 2 π Γ ( 3 2 ) Γ ( 3 1 ) 2 2 3 1 = 5 × 2 3 1 Γ ( 3 2 ) Γ ( 3 1 ) 2 and then the relfection formula Γ ( z ) Γ ( 1 − z ) = π c o s e c π z tells us that A = 5 π 2 3 1 Γ ( 3 1 ) 3 sin 3 1 π = 5 π 2 3 4 3 Γ ( 3 1 ) 3 = 2 0 π 3 3 4 ( − 3 2 ! ) 3 making the answer 4 + 3 + 2 0 − 2 = 2 5