Tricky Corner!
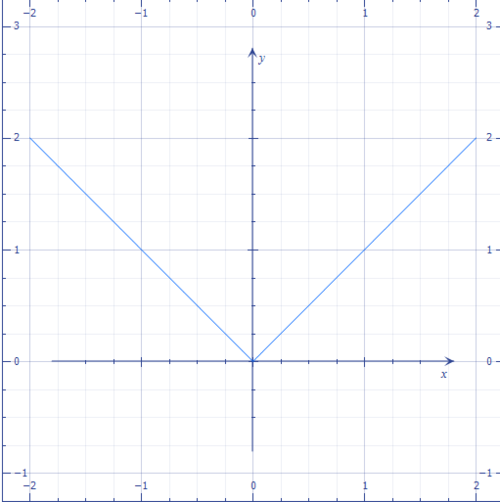 Above shows the graph of
f
(
x
)
=
∣
x
∣
, what is the value of
f
′
(
0
)
?
Above shows the graph of
f
(
x
)
=
∣
x
∣
, what is the value of
f
′
(
0
)
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Another way is to find the one-sided derivatives of f ( x ) at x = 0 . By definition of the absolute value function, we have,
x → 0 − lim f ′ ( x ) = ( − 1 ) and x → 0 + lim f ′ ( x ) = 1
Since the left and right derivatives are unequal, we conclude that f ′ ( 0 ) doesn't exist, ergo, f ( x ) is not differentiable at x = 0 .
Log in to reply
we also can draw infinite number of tangent lines at that point so we cannot determine what is the derivative at x=0
When there is a sharp edge, function cannot be differentiable. here at point 0 there is a sharp edge hence f'(0) is not differentiable.
I think sharp is not so rigorous term. Consider f ( x ) = 1 5 x 4 / 3 − 1 2 x 5 / 3 and see whether it's sharp on x = 0
So I think proofing that the left limit and right limit of the derrivative not the same is the most convincing way yo answer this
Recall that a function is not differentiable at some point x if it has a sharp edge at that particular point.
 as u can see the no. of slopes we can draw through the point 0 hence the slope is not fixed as multiple lines like the above can be drawn!!!
as u can see the no. of slopes we can draw through the point 0 hence the slope is not fixed as multiple lines like the above can be drawn!!!
The function has sharp point on x=0 making it non deferenciable at 0
f ( x ) = ∣ x ∣ = x 2 = ( x 2 ) 2 1 f ′ ( x ) = 2 1 ( x 2 ) − 2 1 × 2 x = ∣ x ∣ x f ′ ( 0 ) = ∣ 0 ∣ 0
∴ N o t d i f f e r e n t i a b l e a t x = 0