Tricky differential
Calculus
Level
pending
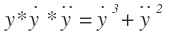If y(0) = 2 and y(1/2) = 2+3e . Find the value of k+m+p if y(5)= k+p*e^m.
Note : Exclude the case of singular solution
Note: y(dot) represents dy/dx y(double dot) represents d2y/dx2
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Putting y' as p.
Now y''= dp/dx or y'' = dp/dy*dy/dx
or y'' = p*dp/dy
Substituting the values in main equation,
we get, y * p * p * dp/dy = p^3 + (p * dp/dy)^2
Again it is Clairaut equation, whose solution can be easily obtained. Rest calculation part, I leave to you all.