Circling Around
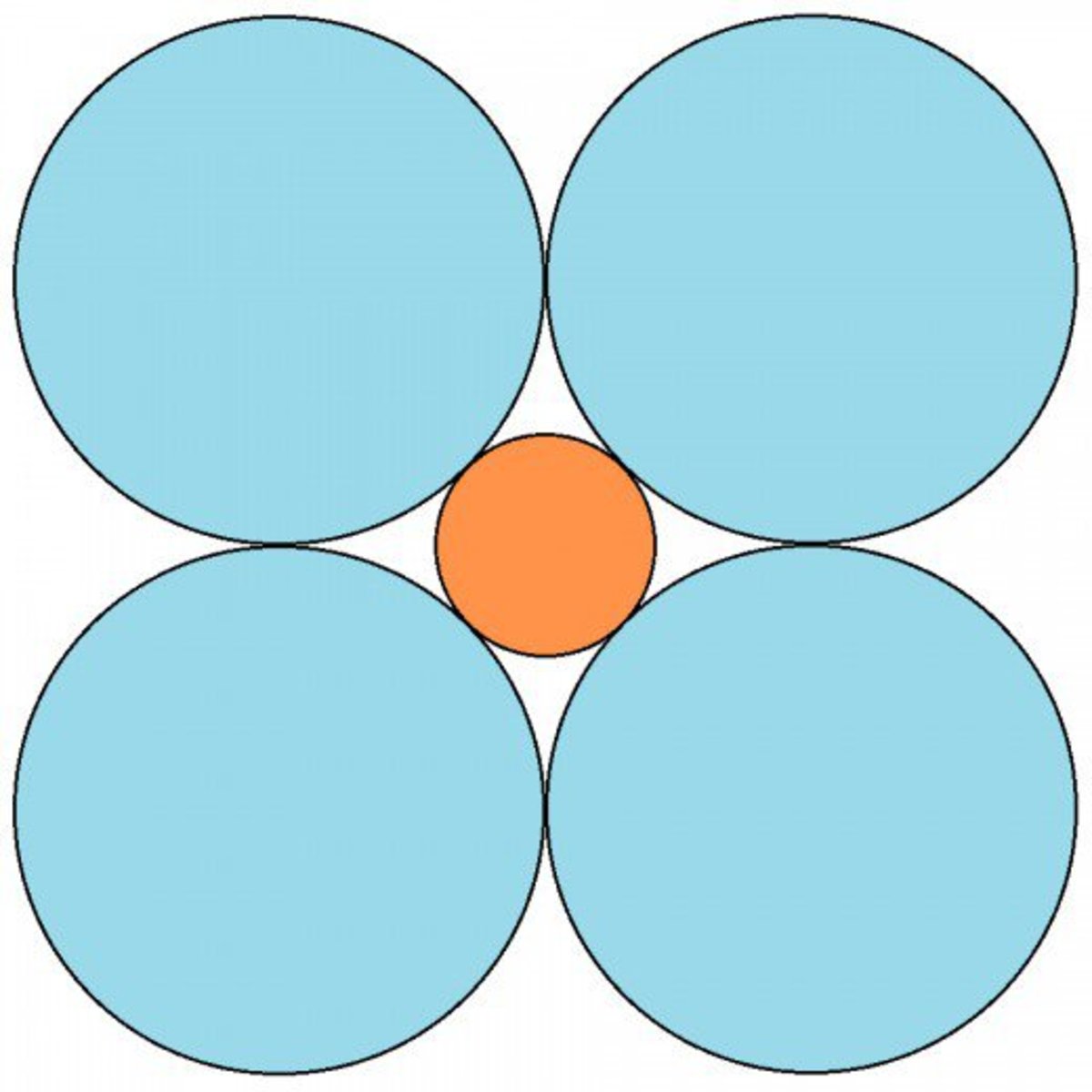
Four circles , each with a radius of 1, are arranged so that they are tangent to two others and their centers form the corners of a square. A smaller circle is inscribed in the space bounded by the four circles, and this smaller circle is tangent to each of the other four. What is its radius?
Give your answer to 3 decimal places.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
If we connect the radius of 4 circles, then we can get a square. The perimeter of the square is 8 because the radius is 1, and the side of the square is 2 times of radius, so the length of the side is 2. So, the perimeter is 8. Then, let the diagonal of the square to a . We get a 2 + b 2 = c 2 by Pythagorean theorem, so 2 2 + 2 2 = a 2 . Then a equals to 2 2 . The radius of big circle is 1, so we subtract 2 from the 2 2 . Then, we get the 2 times of radius of the small circle. It is 2 2 − 2 . Then we get the radius of small circle, 2 2 2 − 2 which is equal to 2 − 1 . So it is 2 − 1 , but we have to give the answer to 3 decimal digits, so it is 1 . 4 1 4 − 1 = 0 . 4 1 4 .
1 + 2r + 1 = 2 sqrt2, 2 + 2r = 2 sqrt2, r = sqrt2- 1, r ≈ 0.41421.