Tricky Lists
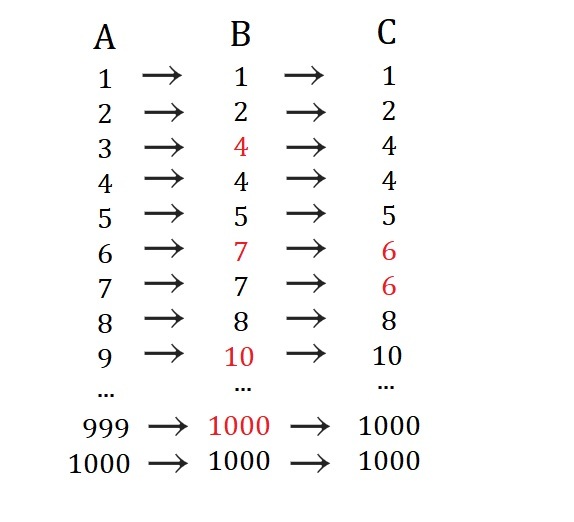
The list is the list of all positive integers from to . We create a list by changing all the multiples of from the list by its successors. Then we create the list by changing all the multiples of from the list by its predecessors.
How many numbers in list still appears at least one time in the list ?
The answer is 620.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
By the time you get to list C, have have lost multiples of 3 and 7 , but regained those multiples of 3 which are 1 less than a multiple of 7 . There are
so there are 3 3 3 + 1 4 2 − 4 7 = 4 2 8 numbers which are multiples of either 3 or 7 . Numbers which are multiples of 3 and also 1 less than a multiple of 7 are of the form 6 + 2 1 k for k ≥ 0 , and so there are 4 8 such numbers. Thus a total of 4 2 8 − 4 8 = 3 8 0 numbers are removed from list A when list C is created, and so there are 6 2 0 different numbers still left in list C.