Tricky Locus

Holditch's theorem states that if a chord of fixed length is allowed to rotate inside a convex closed curve, then the locus of a point on the chord a distance $p$ from one end and a distance $q$ from the other is a closed curve whose enclosed area is less than that of the original curve by $pq\pi$

In this case $p=q=3$ .

$\text{Area enclosed by the locus} = \text{Area of the triangle} -pq\pi = \boxed{84-9\pi}$

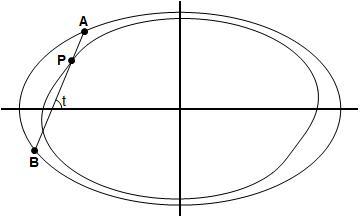
Suppose that $AB$ is a rod of length $p+q$ , and that $P$ is a point on the rod such that $AP = p$ and $PB = q$ . We let $AB$ slide around the triangle in such a manner that, as the points of contact $A$ and $B$ make a full anticlockwise tour around the triangle, the angle $t$ that the rod makes with the $x$ -axis increases from $0$ to $2\pi$ . We now want to know about the locus of $P$ .

If the coordinates of $P$ are $(x,y)$ , where $x,y$ are functions of $t$ , then the coordinates of $A$ and $B$ are $A \; (x + p\cos t,y + p\sin t) \hspace{2cm} B \; (x - q\cos t,y - q\sin t)$ Thus the area of the region swept out by the point $P$ is $X_P \; = \; \tfrac12\int_0^{2\pi} \big(x\dot{y} - \dot{x}y\big)\,dt$ while the area of the region swept out by the point $A$ is $X_A \; = \; \tfrac12\int_0^{2\pi}\big(x+p\cos t)(\dot{y}+p\cos t) - (\dot{x}-p\sin t)(y + p\sin t)\big)\,dt \; = \; X_P + \pi p^2 + pQ$ and the area of the region swept out by the point $B$ is $X_B \; = \; \tfrac12\int_0^{2\pi}\big(x-q\cos t)(\dot{y}-q\cos t) - (\dot{x}+q\sin t)(y - q\sin t)\big)\,dt \; = \; X_P + \pi q^2 - qQ$ where $Q \; = \; \tfrac12\int_0^{2\pi} \big((x+\dot{y})\cos t + (y - \dot{x})\sin t\big)\,dt$ and hence $qX_A + pX_B \; = \; (p+q)X_P + \pi pq(p+q)$ This calculation can be extended to handle the case when the outside curve is only piecewise differentiable, as here In this case $X_A = X_B = 84$ and $p=q=3$ , obtaining the area $X_P = 84 - 9\pi$ , making the answer $9 + 3 = \boxed{12}$ .

Here is a more direct proof of this particular problem. As Steve's diagram shows, for most of the time the rod simply slides along one of the edges, until it has to negotiate a corner of the triangle. Thus $X_P$ is the area of the triangle, minus the three regions missed at the vertices. Suppose that the rod has to move past a vertex of angle $\alpha$ . Suppose that the origin of our coordinate system is at the triangle's vertex, while one side of the triangle lies along the $x$ -axis, while the second side of the triangle lies in the first quadrant portion of $y = x\tan\alpha$ . The the coordinates of the midpoint of the rod, when the rod makes an angle $t$ with the $x$ -axis, are $x \; = \; 3\cos t + 6\cot\alpha \sin t \;,\; y \; =\; 3\sin t \hspace{2cm} 0 \le t \le \pi-\alpha$ In this case $x\dot{y} - \dot{x}y = 9$ , and so the area "missed" at this vertex is $\tfrac92(\pi-\alpha)$ . Thus the area missed as the rod goes around the triangle $PQR$ is $\tfrac92((\pi-P)+(\pi-Q)+(\pi-R)) \; = \; \tfrac92(3\pi-P-Q-R) \; = \; 9\pi$

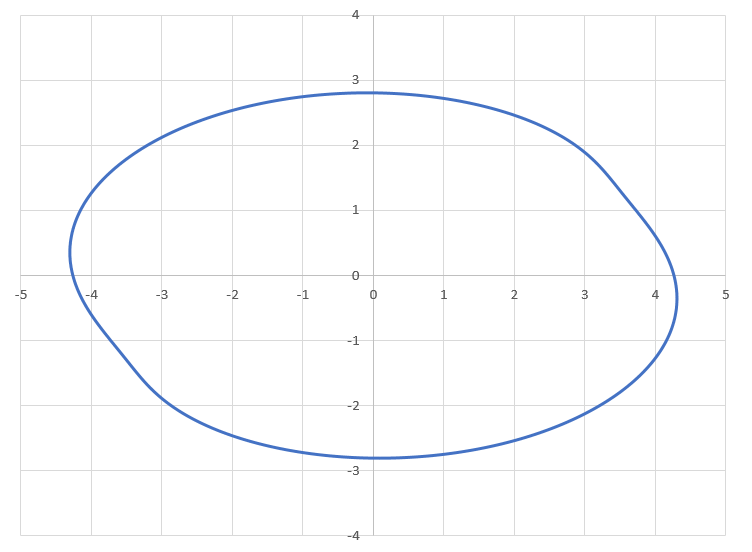
For fun, here is the shape of the locus I got. It looks a bit different from the image in the problem, but the enclosed area turns out to be $12 \pi$ regardless.

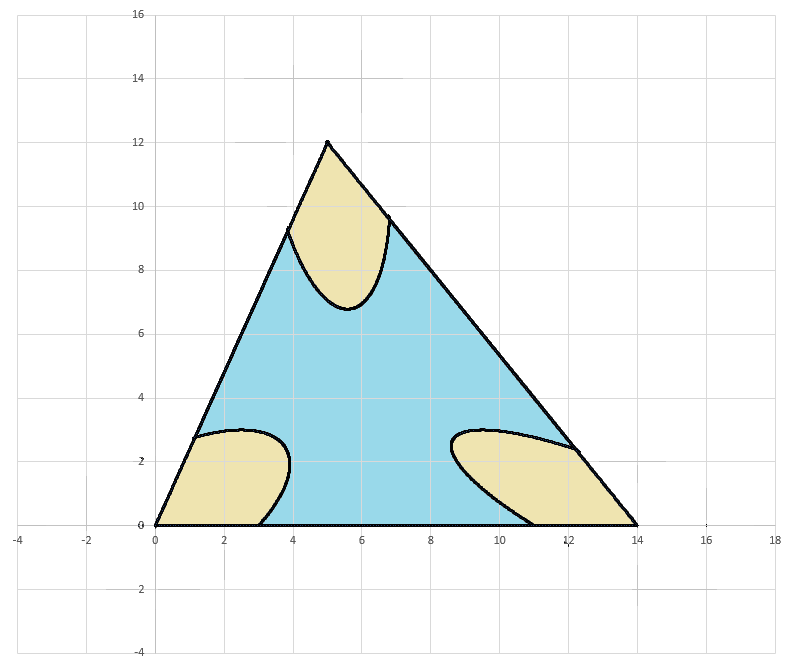
The locus for the revised triangular problem is below:

https://ds055uzetaobb.cloudfront.net/uploads/xAcURemDA4-locus-tri.png