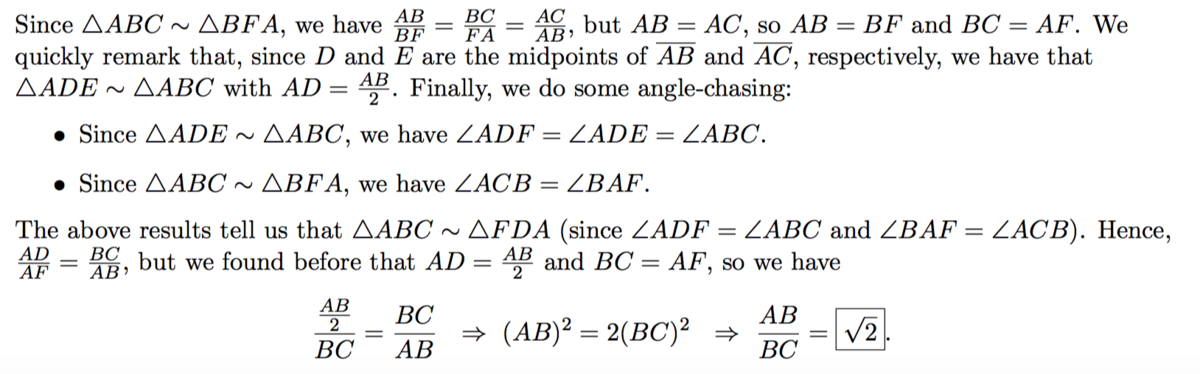Tricky Similar Triangles
If triangle
A
B
C
is similar to triangle
B
F
A
,
then find
B
C
A
B
.
The answer is 1.414.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
nice solution :)
I did it in the same way!!!
Very nice solution. I used a different approach but arrived at a different answer. Please help me find what's wrong. Clearly ABC is congruent to BFA not just similar. Where BF intersects EC call that G. Triangle AGB is isosceles with base angles equal to vertex angles of ABC and BFA. This means external angle EGF is equal to sum of those base angles (angles FBA and CAB). Since ADE is similar to EFG then angle DAE= angle EFG. Therefore we find a triangle ABC with base angle twice the vertex angle. That can only be true if base angles are 72° and the vertex angle is 36°! No draw a perpendicular down from point A to BC and this is the altitude of triangle ABC. The sine of half the angle of the vertex is equal to BC/2 over AB. Well sine of 18° is 0.309. Therefore AB/BC is 1.618. Wish I could leave a diagram but cannot in this field. My email is [email protected]. I could respond with a diagram there. Thank you.
It must be 2
AB/AD=BC/DE=2 SINCE AB=2ADTHAT MEANS AB/BC=AD/DE=2
First the angles
For isosceles ΔABC let b = ∠ABC = ∠ACB <base angles> a = ∠BAC = 90 -b <vertex angle>
By defintion isosceles ΔBFA is similar to ΔABC so ∠BAF = ∠BFA = b
Now consider the smaller ΔADE whose base is parallel to ΔABC’s and is therefore similar to both ΔABC and ΔBFA, so ∠ADE = ∠AED = b
Now consider ΔFAD Since we have already established its base angles ∠DAF(BAF) = b and ∠ADF(ADE) = b ΔFAD is an isosceles triangle similar to the other three, ΔABC, ΔBFA and ΔADE.
Now let’s turn to lengths
Let’s define the base and side lengths of the smaller similar ΔADE as DE = x AD = AE = ax
The base and side lengths of the larger congruent triangles ΔABC and ΔBFA are BC = FA = 2x AB = AC = BF = BA = 2ax
The base and side lengths of the smaller similar ΔFAD is AD = ax FA = FD = 2x
The ratios of a side to base length of each of the four similar triangles must be equal <ΔABC and ΔBFA> AB/BC = BF/FA = 2ax/2x = a < ΔADE> AD/DE = ax/x = a < ΔFAD> FA/AD = 2x/ax = 2/a
So a = 2/a a = AB/BC = sqrt(2) ≈ 1.41
This is a great solution! There is another solution (or two) that does not use trigonometry, though. Can anyone find it?
Log in to reply
solution
solution2
Log in to reply
Loving the diagram. Very helpful indeed :)
please explain how u got ge as 2
thanks @Eli Ross
Nice solution eli rose
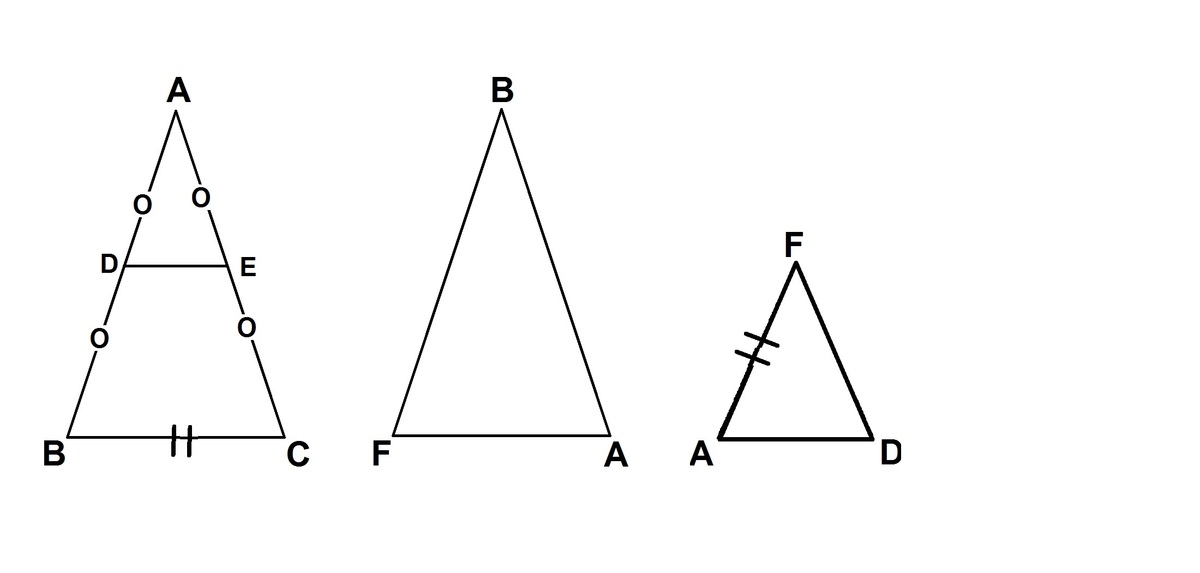
B C F A = A C B A = 1 . ⟹ Δ s A B C ≡ B F A . D E ∣ ∣ B C ∴ ∠ A D F = ∠ A B C = ∠ F A D o f Δ B F A . ∴ Δ s A B C ≡ F A D . B u t B C = F A . ∴ B C A B = A D F A = 2 1 ∗ A B B C . ⟹ B C A B = 2 = 1 . 4 1 4
How you ABF congruent to ABC
Log in to reply
It is given that they are similar. But AB is a common side. Both are isosceles.
If BC =FA, as stated above, then triangles ABC and BFA are not only similar, but congruent. Something is wrong.
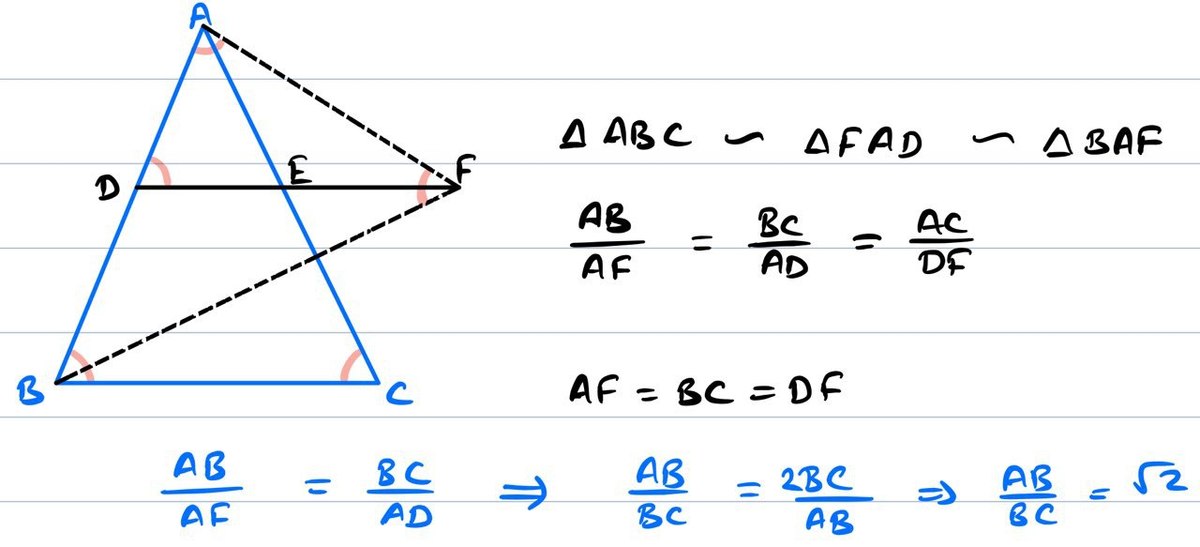
Here's another approach: