Tricky spring balance
Manya hung two blocks of respective masses 1 0 kg and 5 kg .
What is the reading on the spring balance ( in kg ) ?
Assumptions: The pulley and string are both massless and frictionless. The spring balance is calibrated to read the mass of a stationary object hung in the current gravity.
The answer is 13.333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
For the last equation, 40g / g = m
So the reading is wrong? One has effectively reduced mass by hanging it from a string?
Log in to reply
While the two weights are accelerating, the effective mass is reduced.
If the 5kg weight hits the pulley and stops, then the weight will end up as 15kg.
If the weight is not stopped by the pulley then the weight becomes zero.
The implication, even if not explicit, is that the first scenario is the one we are interested in.
Yes because there is acceleration of blocks. This is the same reason when an object is freely falling due to gravity, it experiences weightlessness.
Surely we can't assume that she would read the weight before the system came to equilibrium.
The 5kg block would accelerate to the pulley, get stuck, and the spring would read a combined weight of 15kg.
Unless it's an open pulley in which case the weight would be 0kg after the weights fell off.
Everyone who's answered this question has replied with the initial weight, before the system came to rest - but the question doesn't indicate that we should do that.
Looks great except I think it reaches equilibrium when the 5kg mass reaches the top of the pulley and the 10kg mass reaches the bottom of the rope. At that point it will stop and effectively be a 5kg mass attached to a 10kg mass attached t o a spring scale. Try it and see for yourselves
Call the two hanging masses m 1 , m 2 . The standard analysis of the Atwood machine shows that they accelerate at a 1 , 2 = ± m 1 + m 2 m 1 − m 2 g . Thus their center of mass accelerates at a rate a C M = m 1 + m 2 m 1 a 1 + m 2 a 2 = ( m 1 + m 2 m 1 − m 2 ) 2 g . Apply Newton's Second Law to the system of the two masses plus the pulley; the two forces acting are the upward tension from the scale F s and the downward force of gravity F g = ( m 1 + m 2 ) g , so that F s = F g − F net = ( m 1 + m 2 ) g − ( m 1 + m 2 ) a C M and division by g gives the reading of the scale, g F s = ( m 1 + m 2 ) ( 1 − ( m 1 + m 2 m 1 − m 2 ) 2 ) = m 1 + m 2 4 m 1 m 2 . In this case it is 1 0 + 5 4 ⋅ 1 0 ⋅ 5 = 1 5 2 0 0 = 3 4 0 = 1 3 . 3 3 kg .
'tis always a good learning experience to read your solve posts. JLO
Spring will measure 2T as the weight, where, T is the tension in the string attached to each weight. The equations are( g is acceleration under gravity, a is acceleration of each mass):
(1) T=5g+5a,
(2) 10g=T+10a
Solving, 2T=(40/3)g,
Answer=(40/3)=13.333.
@Vinod Kumar Sir I have a doubt.can you please clear it ?Sir why you not multiplied g in the last step??Please reply.
Log in to reply
Simply, because, the spring balance is going to show 13.333 as the reading.
When we weigh something on weighing machine, the number displayed is without g multiplication.
The net force downward is only 5. So the 10kg block is falling at 5/15=1/3 of its "usual" rate. So the spring will only feel 2/3 of what it would if this weight were at rest. On the other side, the 5kg block is rising at an extra 1/3. So the spring will feel 4/3 of what it would if this block were at rest.
Total felt by the spring: 10(2/3)+5(4/3)=40/3=13.3333
My thinking was very similar. If there was one 5kg block on each side, it would be at rest, and the scale would read 10kg. If you add one 5kg block to one side, that block would add a force of one block but have the inertia of all three. So the extra block accelerates at, as you said, "1/3 the usual rate". So the spring takes the other 2/3 of the force, resulting in 10kg + (2/3)*5kg = 13.333kg.
Relevant wiki: Constraint Relation
After drawing FBD of the two blocks you will get two equations which after solving you will get acceleration and tension in the lower string.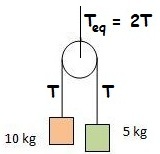 1
0
g
−
T
=
1
0
a
T
−
5
g
=
5
a
a
=
3
g
,
T
=
3
2
0
g
Assuming that the pulley is mass-less, tension in the upper string will be twice the tension in lower string,
T
e
q
=
2
T
=
3
4
0
g
.
1
0
g
−
T
=
1
0
a
T
−
5
g
=
5
a
a
=
3
g
,
T
=
3
2
0
g
Assuming that the pulley is mass-less, tension in the upper string will be twice the tension in lower string,
T
e
q
=
2
T
=
3
4
0
g
.
The reading on a Spring Balance shows the mass acting on it. But here we got tension T e q which is equal to weight acting on spring balance. But, we know that W = m g ⟹ 3 4 0 g = m g
⟹ m = 3 4 0 k g ≈ 1 3 . 3 3 3 k g