Tricky Triangle
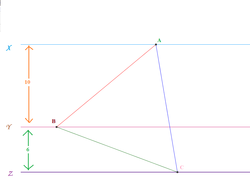 X
,
Y
and
Z
are 3 mutually parallel straight lines in a plane, such that
Y
is between
X
and
Z
and the distance between
X
and
Y
is
1
0
units and the distance between
Y
and
Z
is
6
units.
A
B
C
is an equilateral triangle with
A
on
X
,
B
on
Y
and
C
on
Z
. If the area of
△
A
B
C
can be expressed as
b
a
2
where
a
and
b
are coprime positive integers and
b
is not divisible by the square of any prime, find the value of
a
+
b
.
X
,
Y
and
Z
are 3 mutually parallel straight lines in a plane, such that
Y
is between
X
and
Z
and the distance between
X
and
Y
is
1
0
units and the distance between
Y
and
Z
is
6
units.
A
B
C
is an equilateral triangle with
A
on
X
,
B
on
Y
and
C
on
Z
. If the area of
△
A
B
C
can be expressed as
b
a
2
where
a
and
b
are coprime positive integers and
b
is not divisible by the square of any prime, find the value of
a
+
b
.
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
NICE... ONLY ONE THAT I CAN UNDERSTAND (IT DOESN'T HAS SINE AND COSINE!)
First we draw the line parallel to X Z through B and the perpendiculars from A and C to this line. The first one intersects the line at P , the second at O . If we call the length of each side of the triangle l and the angle ∠ B O C = α , we have ∠ B A P = 6 0 − α and get the following equations:
{ l sin ( α ) = O B = 6 , l sin ( 6 0 − α ) = B P = 1 0 .
We now manipulate the second equation, using the angle sum formula for sines: l sin ( 6 0 − α ) = l ( sin ( 6 0 ) cos ( α ) − cos ( 6 0 ) sin ( α ) ) = l ( 2 3 cos ( α ) − 2 1 sin ( α ) . Since we know l sin α , we can fill this in to obtain l cos α = 3 2 6 . We thus have l 2 = l 2 ( sin 2 α + cos 2 α ) = … = 3 7 8 4 . Since the area of an equilateral triangle given a side l equals 4 3 l 2 , it follows that A = 4 3 ⋅ 3 7 8 4 = 3 1 4 2 and thus the answer is 1 4 + 3 = 1 7 .
Nice exactly how i did it.
Let B be the origin of the complex plane then C is the complex number t − 6 i . We rotate C round B and get A , that is
A = C ( 2 1 + 2 3 i ) = ( t − 6 i ) ( 2 1 + 2 3 i ) = ( 2 t + 6 3 ) + ( 2 t 3 − 3 ) i
Because the y coordinate of A is 10, that means 2 t 3 − 3 = 1 0 , then t = 3 2 6 3
The area of the A B C is 4 B C 2 3 , so we have
S A B C = 4 ( t 2 + 3 6 ) 3 = ( ( 3 2 6 3 ) 2 + 3 6 ) 4 3 = 3 1 3 2 + 2 7 = 3 1 4 2
This is how I did it.
I'm not exactly sure why the problem creator decided to put b a 2 instead of just b a or even c a b .
Let s be the sides of the triangle. Make a vertical line passing through vertex B .
From vertex B , let
θ be the angle between the upper vertical line X Y to the side B A .
α be the angle between the lower vertical line Y Z to the side B C .
θ + 6 0 + α = 1 8 0 ; θ + α = 1 2 0
cos θ = s 1 0
s = cos θ 1 0
cos α = s 6
s = cos α 6
1 0 cos θ = 6 cos α
1 0 cos ( 1 2 0 − α ) = 6 cos α
cos 1 2 0 c o s α + sin 1 2 0 sin α = 3 5 cos α
Simplifying can arrive
tan α = 6 3 2 6
tan α = 6 3 2 6 = 6 2 6 / 3 = Y Z Z A
s = ( Z A ) 2 + ( Y Z ) 2
s = ( 2 6 / 3 ) 2 + ( 6 ) 2
s = 3 2 8 3
Solving for the area of the triangle A
A = 2 1 s 2 sin 6 0
Substituting values:
A = 3 3 9 2 . 2 3 = 3 1 4 2
a + b = 1 4 + 3 = 1 7
Draw a line perpendicular from B to line X and to line Z , name the intersection points D and E ; and draw a line perpendicular from C to line X , name the intersection point F . Clearly a rectangle is formed. Name L the side lenght of the triangle, a = D A and b = A F . The dimentions of the rectangle are: height of 1 6 and base x + y . Apply Pythagorean Theorem to triangles △ B D A , △ B E C and △ A F C : 1 0 2 + x 2 = L 2 6 2 + ( x + y ) 2 = L 2 y 2 + 1 6 2 = L 2 Solve for x and y from first and third equations and substitute in the second one: x = L 2 − 1 0 0 y = L 2 − 2 5 6 3 6 + ( L 2 − 1 0 0 + L 2 − 2 5 6 ) 2 = L 2 3 6 + L 2 − 1 0 0 + 2 ( L 2 − 1 0 0 ) ( L 2 − 2 5 6 ) + L 2 − 2 5 6 = L 2 2 L 4 − 3 5 6 L 2 + 2 5 6 0 0 = 3 2 0 − L 2 4 ( L 4 − 3 5 6 L 2 + 2 5 6 0 0 ) = ( 3 2 0 − L 2 ) 2 4 L 4 − 1 4 2 4 L 2 + 1 0 2 4 0 0 = 1 0 2 4 0 0 − 6 4 0 L 2 + L 4 3 L 4 − 7 8 4 L 2 = 0 3 L 2 = 7 8 4 L 2 = 3 7 8 4 Finally, the area of an equilateral triangle of side L is A = L 2 4 3 : A = 3 7 8 4 × 4 3 A = 3 1 9 6 = 3 1 4 2 Hence, a = 1 4 , b = 3 and a + b = 1 7 .