Tricky Triangle
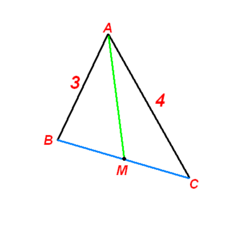 Δ
A
B
C
has
A
B
=
3
, and
A
C
=
4
, and is such that
B
C
=
A
M
, where
M
is the midpoint of
B
C
. What is the length of side
B
C
?
Δ
A
B
C
has
A
B
=
3
, and
A
C
=
4
, and is such that
B
C
=
A
M
, where
M
is the midpoint of
B
C
. What is the length of side
B
C
?
The answer is 3.162.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
It is a direct application of Stewart's theorem , the proof of which is simple using Law of Cosines (see the proof in Wikipedia).
I used it here, but here's another way I thought of after solving: you could create a parallelogram by adding a triangle (let it be △ B C D ) congruent to △ A B C with common side B C . Let α : = ∠ A .
Using law of cosines on △ A B C , △ A C D , knowing cos ( 1 8 0 − α ) = − cos α and 4 B C 2 = A D 2 , we get
4 ( 3 2 + 4 2 − 2 ⋅ 3 ⋅ 4 ⋅ cos α ) = 4 2 + 3 2 + 2 ⋅ 4 ⋅ 3 ⋅ cos α
Solve for cos α , then apply law of cosines on △ A B C to find B C .
By Apollonius' theorem
3 2 + 4 2 = 2 1 B C 2 + 2 A M 2
As B C = A M
3 2 + 4 2 = 2 1 B C 2 + 2 B C 2
2 5 = 2 5 B C 2
B C = 1 0
Construction:
Extend AM to point D such that A M = M D . Thus forming a parallelogram ABDC (This is easy to show using congruent triangles).
Now, in a parallelogram, it is a well-known fact (which is also very easy to prove) that the sum of the squares of the two diagonals is equal to twice the sum of the squares of the two adjacent sides of the parallelogram.
Hence, if B C = x , then
x 2 + ( 2 x ) 2 = 2 ( 3 2 + 4 2 )
therefore,
5 x 2 = 5 0
And finally,
x = 1 0 = 3 . 1 6 2