Tricky Triangles
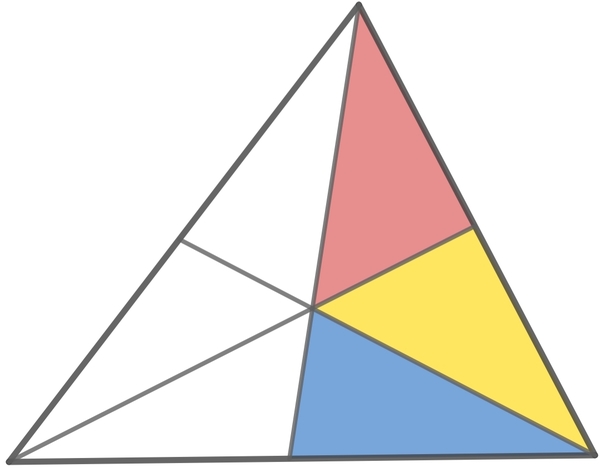
The figure shows a triangle divided into six regions using line segments drawn from the vertices to the opposite sides.
The red and blue regions have the same areas of 1 unit.
What should be the area of the yellow region so that the area of the whole triangle is minimum?
The answer is 1.6917395.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Digvijay Singh how did you create this image?
Use
Menelaus' theorem
to represent the area of the whole triangle by the area of yellow region. Define it as X.
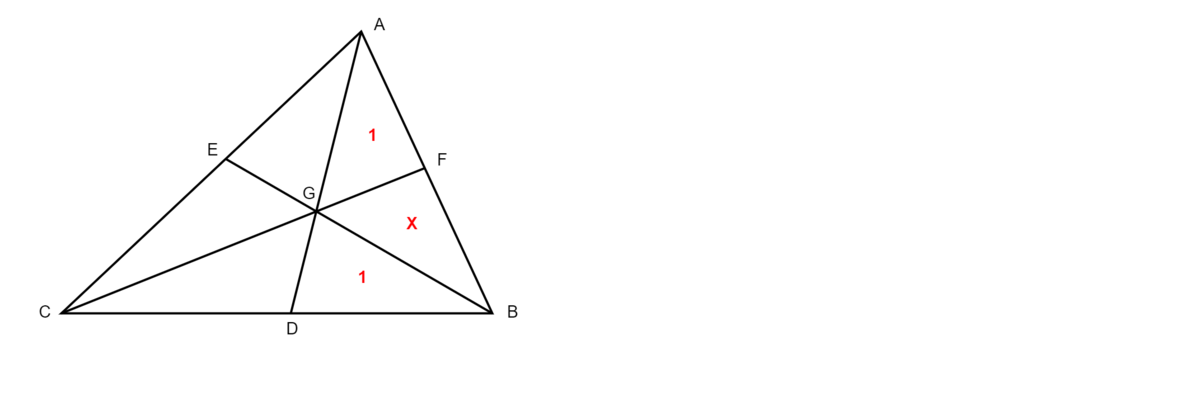 Use Menelaus's theorem on
△
A
B
D
, so we get:
Use Menelaus's theorem on
△
A
B
D
, so we get:
C D ⋅ G A ⋅ F B B C ⋅ D G ⋅ A F = 1
Introduce area relationships, we get:
[ S − ( 2 + X ) ] ⋅ ( 1 + X ) ⋅ X S ⋅ 1 ⋅ 1 = 1
We can figure out S
S = X 2 + X − 1 X ( 1 + X ) ( 2 + X )
Define the areas X = Δ P L B , Y = Δ P N B , Z = Δ P N A
α = Δ P M A , β = Δ P M C , γ = Δ P L C , S = Δ A B C
From the figure, S = X + Y + Z + α + β + γ , the goal is to find X + Y + Z
We know that the areas of triangles with equal altitudes are proportional to the bases of the triangles.
So, B L C L = X γ = X + Y + Z α + β + γ
and C M A M = β α = β + γ + X α + Z + Y = X + γ Y + Z
where the last equality follows because if b a = d c , then b a = b ± d a ± c
The two expressions imply
X + Y + Z = ( γ α + β + γ ) X
and Y + Z = β α ( X + γ )
solving these equations gives X = β ( α + β ) − α γ α γ 2
⟹ X + Y + Z = β ( α + β ) − α γ α γ ( α + β + γ )
Finally, S = X + Y + Z + α + β + γ = β ( α + β ) − α γ β ( α + β ) ( α + β + γ )
Putting α = γ = 1 , we get
S = β ( β + 1 ) − 1 β ( β + 1 ) ( β + 2 )
which is minimum when β ≈ 1 . 6 9 1 7 3 9 5