Tricky Triangle Analysis
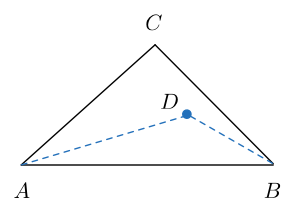 Triangle
A
B
C
has
A
C
=
B
C
,
∠
A
C
B
=
9
6
∘
.
D
is a point in
A
B
C
such that
∠
D
A
B
=
1
8
∘
and
∠
D
B
A
=
3
0
∘
. What is the measure (in degrees) of
∠
A
C
D
?
Triangle
A
B
C
has
A
C
=
B
C
,
∠
A
C
B
=
9
6
∘
.
D
is a point in
A
B
C
such that
∠
D
A
B
=
1
8
∘
and
∠
D
B
A
=
3
0
∘
. What is the measure (in degrees) of
∠
A
C
D
?
The answer is 78.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Y U So Smart
Very intelligent approach to solve this tricky problem ! congratulations !!! K.K.GARG.India
Extremely clever solution!!
CLEVER!!!!!
Excellent; what a beautifully clean proof.
By angle sum property of triangle one will find that a n g l e C A D is 2 4 ° and a n g l e A D B is 1 3 2 ° . Let angle A C D be x . Then angle A D C will be 1 5 6 − x . Let's assume that A B = 1 . Then by applying law of sines for triangle ABC we have A C / s i n 4 2 = 1 / s i n 9 6 . A C = s i n 4 2 / s i n 9 6 . Again by applying law of sines for traingle ABD we find that A D = 1 / 2 s i n 4 8 . After using law of sines in triangle ACD we have the following equation: 1 / ( 2 s i n 4 8 ∗ s i n x ) = s i n 4 2 / ( s i n 9 6 ∗ s i n ( 1 5 6 − x ) ) . After simplification we are left with s i n ( 1 5 6 − x ) = s i n x . By comparison x = 1 5 6 − x or x = 7 8 °
CAD is 24º. Them draw the bissector CH of angle ACB and let AD intersect CB in N. Draw the bissector AS of angle CAN and Let it intersect CH in K. Notice triangle AK = KB, angle HKB = BKS = SKC = 60º; Angles AKC = AKD = 120º then triangles ACK and ADK are congruents by SAS, and because it, CK = KD. Notice KS is bissector of triangle isosceles CKD. Let M be the midpoint of CD, and we have angle KMC = 90º, and angle KCM = 30º. As angle ACD = ACK + KCM, we have angle ACD = 48º + 30º = 78º.
A faster to finish once you find that triangles ACK and ADK are congruent is to note that AC = AD, so triangle ACD is isosceles, so angle ACD = (180-24)/2 = 78.
We claim that ∠ A C D = 7 8 ∘ .
To prove this, let D ′ be the point in triangle A B C such that ∠ D ′ A B = 1 8 ∘ and ∠ D ′ C A = 7 8 ∘ . This implies ∠ D ′ A C = 2 4 ∘ and ∠ A D ′ C = 7 8 ∘ , so triangle A C D ′ is isosceles with A D ′ = A C . Now construct E such that C A D ′ E is a parallelogram. Since A D ′ = A C , it is in fact a rhombus. Furthermore ∠ E C B = 1 8 0 ∘ − 9 6 ∘ − 2 4 ∘ = 6 0 ∘ and E C = B C , so triangle B C E is in fact equilateral.
Next, note that ∠ D ′ E C = ∠ D ′ A C = 2 4 ∘ , so ∠ D ′ E B = 6 0 ∘ − 2 4 ∘ = 3 6 ∘ . Since triangle D ′ E B is isosceles, it follows that E B D ′ = 7 2 ∘ . Finally, ∠ D ′ B C = 7 2 ∘ − 6 0 ∘ = 1 2 ∘ which means ∠ D ′ B A = 3 0 ∘ . Since there is a unique point P in triangle A B C satisfying ∠ P A B = 1 8 ∘ and ∠ P B A = 3 0 ∘ , we conclude that D ′ = D , so ∠ A C D = ∠ A C D ′ = 7 8 ∘ .
Or we could just solve this problem using Trig Ceva.
I use rotated sinus theorem
B e c a u s e Δ A B C i s i s o s c e l e s w i t h v e r t e x ∠ 9 6 o , ∠ D A C = 2 4 o a n d ∠ D B C = 1 2 o . A l s o ∠ B D A = 1 8 0 − 1 8 − 3 0 = 1 3 2 o . I f ∠ C D A = X , a n g l e C D B = 2 2 8 − X . A p p l y i n g S i n L a w t o Δ s C A D a n d C D B , S i n A D C S i n C A D = C A C D = C B C D = S i n C D B S i n D B C . ⟹ S i n ( 2 2 8 − X ) S i n 2 4 = S i n X S i n 1 2 . E x p a n d i n g S i n ( 2 2 8 − X ) a n d S i n 2 A = 2 S i n A ∗ c o s A , o n s i m p l i f y i n g , C o t X = S i n 2 2 8 2 c o s 1 2 1 + C o s 2 2 8 . ⟹ X = 7 8 o . ∴ ∠ A C D = 3 6 0 − 2 4 − 7 8 = 7 8 o
assume acd to be x, angle cad is 24,side ad is given by applying sine rule in triangle adb,given by a sin30/sin132,where a=ab.use sine rule for side ad and ac ,ac is given by a sec42/2,sine rule in triangle acd simplifies into sin(156-x)=sinx. 156-x=x x=78
We will prove A C = A D , which will allow to easily obtain the requested angle.
By interior angle sum in triangle A B C we easily get ∠ C A B = ∠ C B A = 4 2 ∘ . Construct equilateral triangle A B E such that C lies inside it. In order to prove A C = A D we will prove triangles A C E and A D B are congruent.
Since ∠ B A E = 6 0 ∘ we get ∠ C A E = ∠ E A B − ∠ C A B = 6 0 ∘ − 4 2 ∘ = 1 8 ∘ .
We know C A = C B , which imples C lies on the perpendicular bisector of A B , therefore, since triangle A B E is equilateral, we have ∠ C E A = ∠ C E B = 3 0 ∘ .
Therefore, since ∠ C A E = ∠ D A B = 1 8 ∘ , ∠ A E C = ∠ A B D = 3 0 ∘ and A B = A E , we get that triangles A B D and A E C are congruent by ASA, which implies:
A C = A D
Therefore ∠ A C D = ∠ A D C , and since ∠ C A D = ∠ C A B − ∠ D A B = 4 2 ∘ − 1 8 ∘ = 2 4 ∘ , by interior angle sum in triangle A C D we get
∠ A C D = 2 1 8 0 ∘ − 2 4 ∘ = 7 8 ∘ .