Tricky Trigonometry (Mathathon Problem 9)

By the identity $\sin^2{x}+\cos^2{x}=1$

We can divide both sides by $\sin^2 x$ and $\cos^2 x$ to get the following identities respectively:

• $1+\cot^2{x}=\cosec^2{x}$

• $1+\tan^2{x}=\sec^2{x}$

---

$\begin{aligned} \sec^2({\tan^{-1}2})=1+\tan^2({\tan^{-1}2})=1+4&=5\\ \cosec^2({\cot^{-1}3})=1+\cot^2({\cot^{-1}3})=1+9&=10\\ \hline \\ \sec^2({\tan^{-1}2})+\cosec^2({\cot^{-1}3})&=\boxed{15} \\ \end{aligned}$

Using ,

$\textcolor{#20A900}{sec^{2}-tan^{2}=1}$

$\textcolor{#20A900}{cosec^{2}-cot^{2}=1}$

To simplify our question as

$\textcolor{#D61F06}{1+tan^{2}(tan^{-1}(2)) +1+cot^{2}(cot{-1}(3))}$

Since,

$\textcolor{#20A900}{tan(tan^{-1}(x))=(x)}$

$=>$ $\textcolor{#3D99F6}{tan^{2}(tan^{-1}(2))}$ = $\textcolor{#3D99F6}{2^{2}}$

||ly $\textcolor{#3D99F6}{cot^{2}(cot^{-1}(3))}$ = $\textcolor{#3D99F6}{3^{2}}$

Plugging in the above values it becomes,

$\textcolor{#69047E}{1+4+1+9}$

Now comes the trickiest part which I m unqualified for explaining ,but it gives us the ans

15 in the end

First, let's break the equation into two parts, $\sec^2(\tan^{-1} 2)$ and $\cosec^2(\cot^{-1} 3)$ . Making a graph so we can understand the first part better, we get
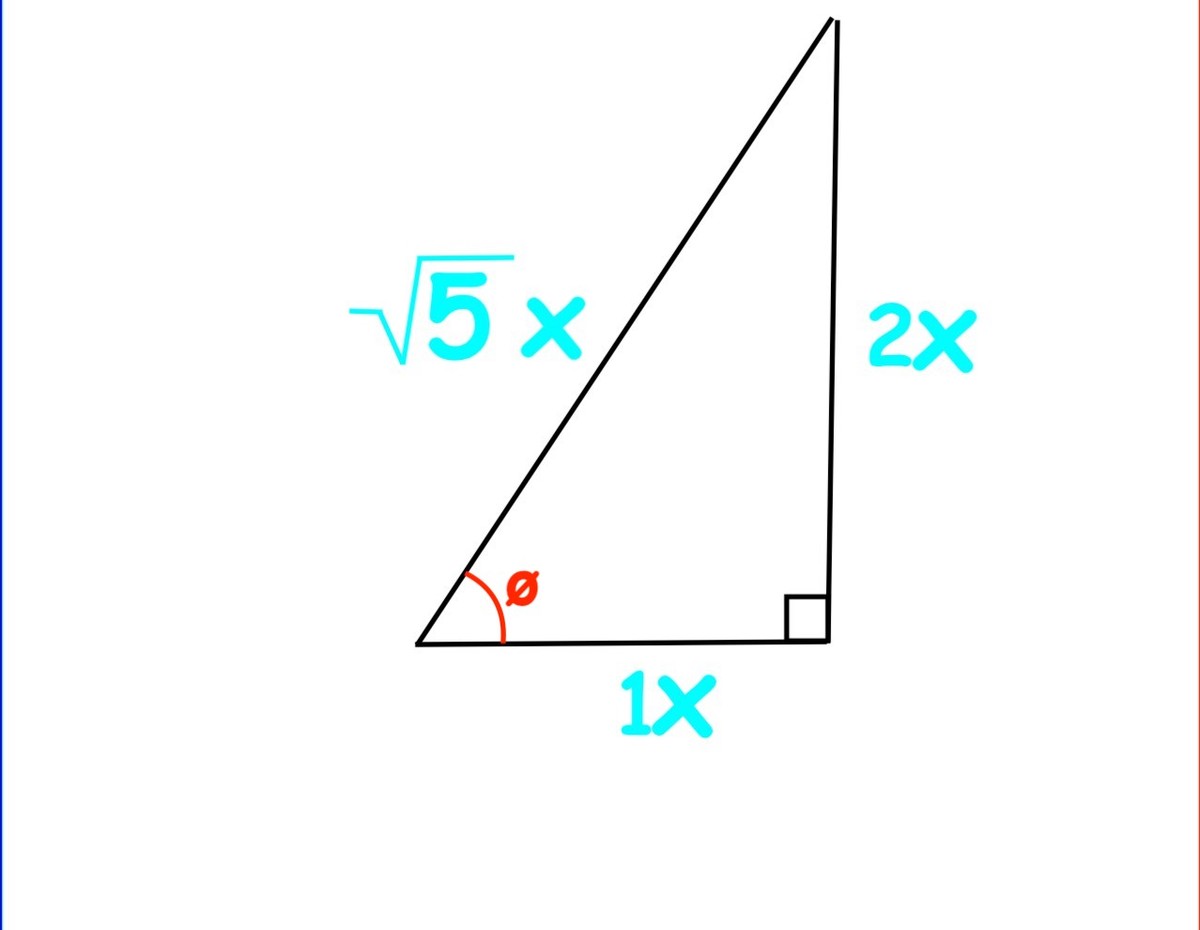(Since the side ratio is 2:1 because of the $\tan^-1$ )Because we don't know the exact length of the sides, we multiply every side by a real number $x$ , so we can account for triangles similar to a 1-2- $\sqrt 5$ triangle. Since $\tan^-1$ is the function for reversing $\tan$ , the output of $\tan^{-1} 2$ is the red $\theta$ in the bottom left corner of the triangle. Because $\sec$ is $\frac{1}{\cos}$ , the secant of $\theta$ is the $\dfrac{\text{hypotenuse}}{\text{adjacent side}}$ , which is just $\sqrt 5$ . Since we have to square this, the output of the first part of the expression is $\boxed 5$ .
Doing the same with the second part of the expression, we get
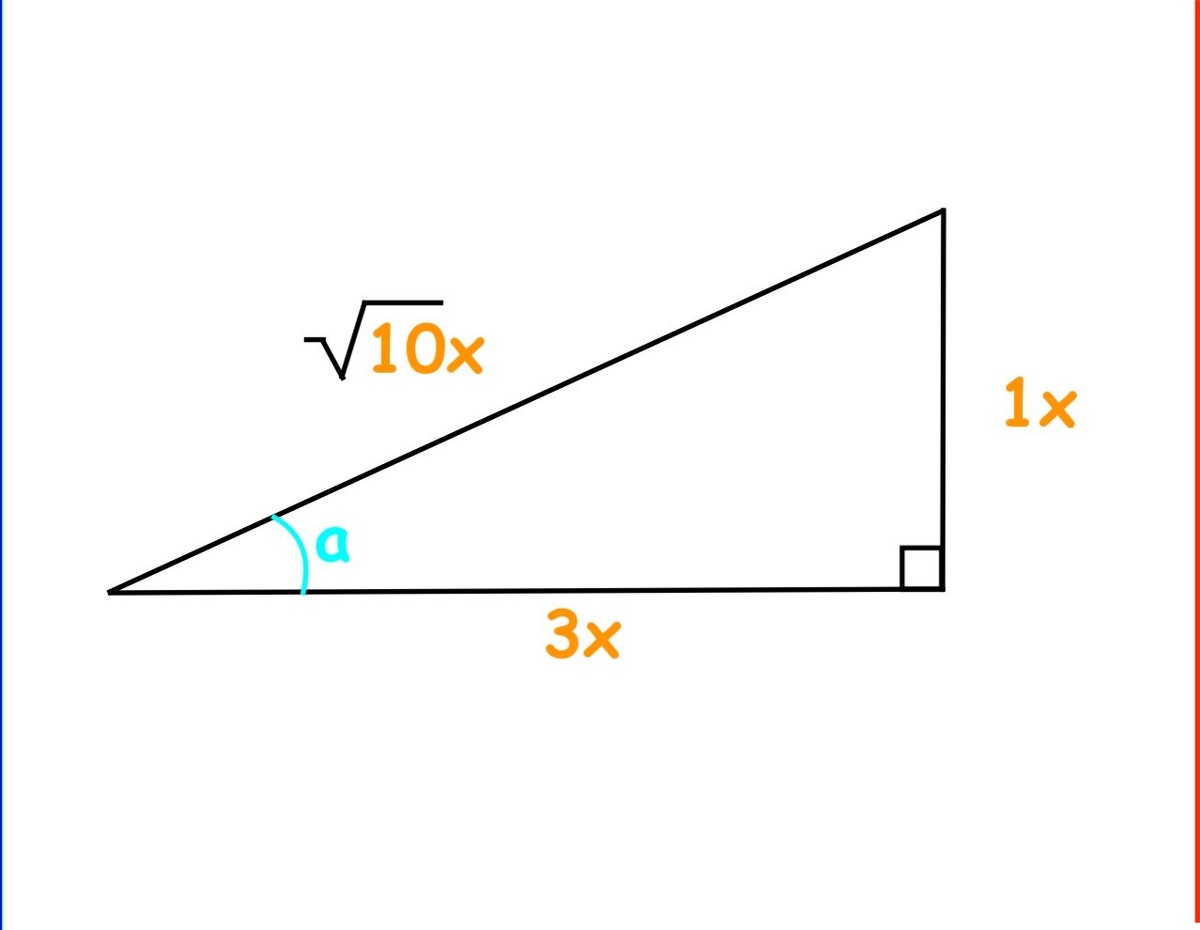In this case, the aqua $a$ is the output of $\cot^{-1} 3$ . Since $\cosec$ is the opposite of $\sin$ , $\cosec a$ is equal to $\frac{\sqrt{10}x}{1x}=\sqrt 10$ . $\cosec^{2} a=10$ , so the second part of the expression is equal to $\boxed {10}$ .
Adding the $5$ from the first part, and the $10$ from the second, we get $5+10=15$ , so our final answer's $\boxed{15}$ .

First of all, let's call $\arctan(2):=\alpha$ and $\text{arccot}(3):=\beta$ . Next, we note that $\sec^2(\alpha) = \frac{1}{\cos^2(\alpha)} = \frac{ \cos^2(\alpha) + \sin^2(\alpha)}{\cos^2(\alpha)} = 1+\tan^2(\alpha)$ and by a similar argument $\csc^2(\beta) = \frac{1}{\sin^2(\beta)} = \frac{ \sin^2(\beta) + \cos^2(\beta)}{\sin^2(\beta)} = 1+\cot^2(\beta).$ Now this helps a lot, since $\begin{aligned} \arctan(2) &=\alpha &\mid \tan()\\ 2 &= \tan(\alpha) &\mid ()^2\\ 4 &= \tan^2(\alpha) &\mid +1\\ 5 &=1+ \tan^2(\alpha) \end{aligned}$
and $\begin{aligned} \text{arccot}(3)&=\beta & \mid \cot()\\ 3 &= \cot(\beta) &\mid ()^2\\ 9 &= \cot^2(\beta) &\mid +1\\ 10 &=1+ \cot^2(\beta) \end{aligned}$ therefore $\sec^2(\alpha) + \csc^2(\beta) = 1+\tan^2(\alpha)+1+\cot^2(\beta) = 5+10 = \boxed{15}.$

Note that for any right angled triangle, say $\triangle ABC$ with $\angle B=90°$ , we have by Pythagoras Theorem,

$\text{AC}^2= \text{AB}^2 + \text{BC}^2$

And dividing the given theorem, on both sides, by hypotenuse squared, i.e $\text{AC}^2$ , we get,

$\dfrac{\text{AB}^2}{\text{AC}^2} + \dfrac{\text{BC}^2}{\text{AC}^2}=1$

But in the right angled triangle, we define $\dfrac{\text{AB}^2}{\text{AC}^2}$ as $(\sin C)^2$ and $\dfrac{\text{BC}^2}{\text{AC}^2}$ as $(\cos C)^2$ for an angle $\angle C$ , which gives,

$\sin ^2 \theta + \cos ^2 \theta =1$

Which holds true for all values of $\theta$ . If we divide the above found equality by $\sin ^2 \theta$ or $\cos ^2 \theta$ , each gives us the following two identities,

$\cot^2 \theta +1 = \cosec^2 \theta$ $\tan^2 \theta +1 = \sec^2 \theta$

Thus for the problem $\red{\sec^2(\tan^{-1}2) + \cosec^2(\cot^{-1}3)}$ , $\tan^{-1}2$ and $\cot^{-1}3$ are the angles applying to which the formulae above, we have,

$\tan^2(\tan^{-1}2) +1 + \cot^2(\cot^{-1}3)+1$

Using the fact that $\text{cif}$ , short for any circular function, $\text{cif}(\text{cif}^{-1}a)= a$ and that $\text{cif}^2 \theta= \text{cif} \theta × \text{cif} \theta$ we get,

$(3×3)+1 +(2×2)+1$

$=\boxed{15}$

We have to use the following identities :

1 + tan^2(x) = sec^2(x)...(1) and

1 + cot^2(x) = cosec^2(x) ...(2)

Proof of (1) :

LHS = 1 + (sin^2(x) / cos^2(x)) = (cos^2(x) + sin^2(x)) / cos^2(x) = 1 / cos^2(x) = sec^2(x)

Similarly, in the case of (2) :

LHS = 1 + (cos^2(x) / sin^2(x)) = (sin^2(x) + cos^2(x))/sin^2(x) = 1 / sin^2(x) = cosec^2(x)

Now let tan(x1) = 2 ...(3) and cot(x2) = 3 ...(4)

We need to find the value of :

sec^2(x1) + cosec^2(x2)

Using identities (1) and (2), we find

sec^2(x1) + cosec^2(x2) = 1 + tan^2(x1) + 1 + cot^2(x2) = 1 + 2^2 + 1 + 3^2 (Using (3) and (4)) = 5 + 10 = 15

For the left part of the expression, a point with the required tangent is at coordinates (1,2). That point is (by pythagorian theorem) at a distance $\sqrt{5}$ from the origin. The secant is therefore $\sqrt{5}/ 1$ and the left part of the sum has a value of 5.

For the right part, a point with the required cotangent at coordinates (3,1). That point is at distance $\sqrt{10}$ from the origin, and therefore the cosecant is $\sqrt{10} / 1$ and the right part of the sum has a value of 10.

The answer is 5 plus 10, or 15.

$\color{#EC7300}{sec^2(tan^{-1}~2})$ + $\color{#3D99F6}{cosec^2(cot^{-1}~3)}$ $=~?$

In right-angled triangle, $tan = \dfrac{Opposite~side}{Adjacent~side}$ . Let $\angle \alpha = tan^{-1}2$ . This is represented in the following right angled triangle.

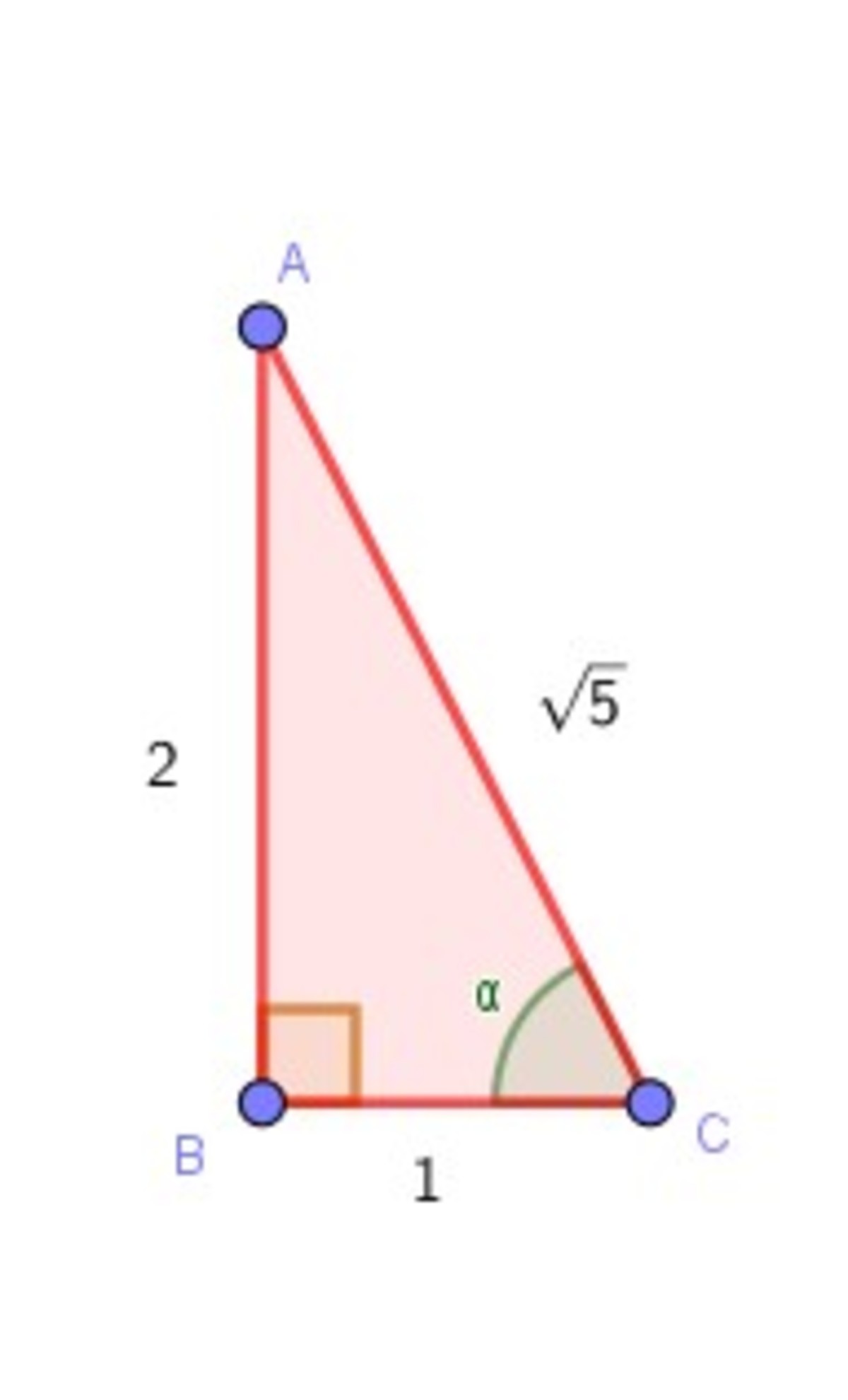
Using $Pythagoras~Theorem$ , hypotenuse = $\sqrt{5}$

$sec ~ \alpha = \dfrac{Hypotenuse}{Adjacent} = \dfrac{\sqrt{5}}{1}$

Therefore, $\color{#EC7300}{sec^2 (tan^{-1}~2)} = 5$

---

In right-angled triangle, $cot = \dfrac{Adjacent~side}{Opposite~side}$ . Let $\angle \beta = cot^{-1}3$ . This is represented in the following right angled triangle.

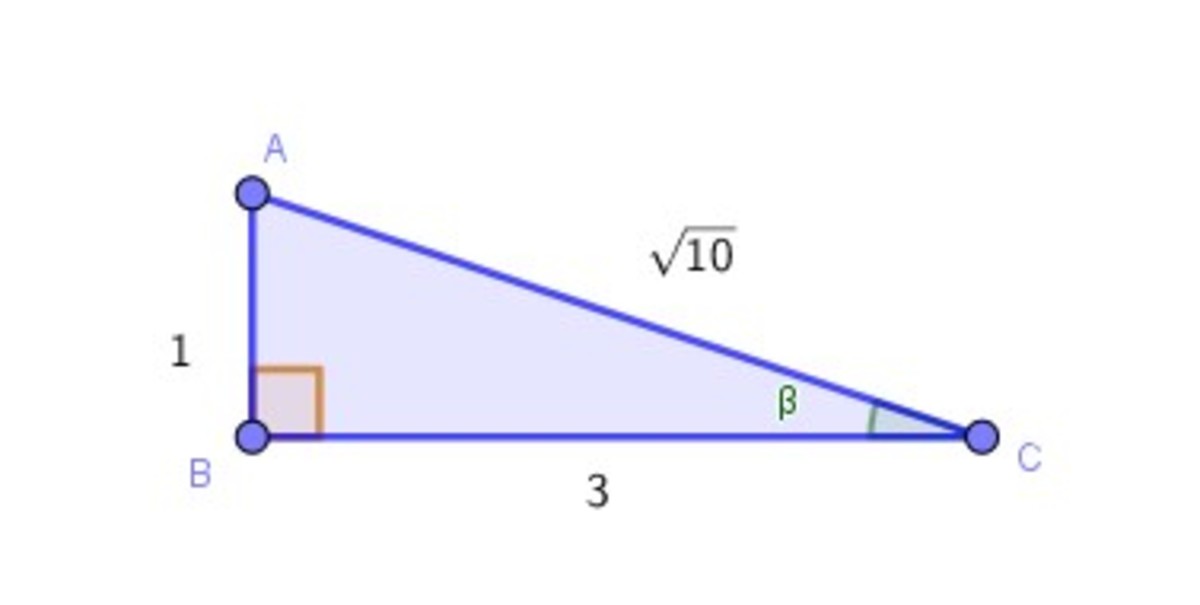
Using $Pythagoras~Theorem$ , hypotenuse = $\sqrt{10}$

$cosec ~ \beta = \dfrac{Hypotenuse}{Opposite} = \dfrac{\sqrt{10}}{1}$

Therefore, $\color{#3D99F6}{cosec^2 (cot^{-1}~3)} = 10$

---

$\color{#EC7300}{sec^2(tan^{-1}~2})$ + $\color{#3D99F6}{cosec^2(cot^{-1}~3)}$ $=5+10=15$

NOTE: Any triangles similar to the given triangles will also give the same result

First let $\tan^{-1}(2)$ = x , then sec²( $\tan^{-1}(2)$ ) = sec²(x)

Since tan(x) = 2
$\frac{\normalsize\sin(x)}{\normalsize\cos(x)}$ = $\frac{2}{1}$
Assuming sin(x) = 2k and cos(x) = 1k

Now using sin²(x) + cos²(x) = 1, we get
$\begin{aligned} 1&= 4k² + k²\\ &= 5k²\\ k²&= \frac{1}{5}\\ k&= \frac{1}{5^{0.5}} \end{aligned}$

Now we get cos(x) as $\pm$ $\frac{1}{5^{0.5}}$ .

Then,
$\begin{aligned} \sec(x)&= \pm5^{0.5}\\ \sec^2(x)&= 5. \end{aligned}$

Therefore sec²( $\tan^{-1}(2)$ ) = 5.
A similar procedure can be used to obtain cosec²( $\cot^{-1}(3)$ ) = 10.
Then the answer is 5 + 10 = 15.

$A=\blue{\sec^2(\tan^{-1}2)}+\red{\cosec^2(\cot^{-1}3)}$ $let\space x=\blue{\tan^{-1}2}\Rightarrow \blue{\tan x=2}$ $\Rightarrow 4=\tan^2 x = \sec^2 x - 1\Rightarrow 5= \sec^2 x$ $\Rightarrow \blue{\sec^2(\tan^{-1}2) = 5}$ $let\space y=\red{\cot^{-1}3}\Rightarrow \red{\cot y=3}$ $\Rightarrow 9=\cot^2 y = \cosec^2 y - 1\Rightarrow 10= \cosec^2 y$ $\Rightarrow \red{\cosec^2(\cot^{-1}3) = 10}$ $\Rightarrow A=\blue{5}+\red{10}=\boxed{\red{1}\blue{5}}$