Tricky Tripping Triangular Triplet
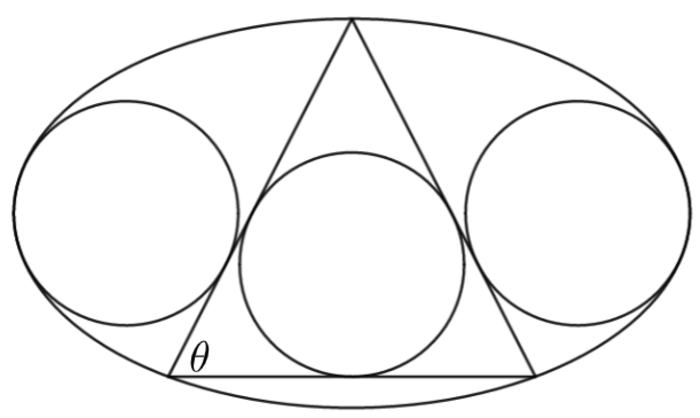
In the nondegenerate ellipse, two identical circles both of maximum possible area are positioned, such that each of them shares one point of tangency with the ellipse at their respective end. The isosceles triangle whose bottom base is parallel to the major axis and whose apex point lies on the ellipse is positioned tangent to those circles. There exists a base angle , such that the incircle of the triangle has the same radius as either of the two circles.
If is in radians, input as your answer.
The answer is 1097375.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Quite an interesting problem. To solve this we first consider an ellipse of major axis of length 2 a along the x − a x i s and minor axis of length 2 b along the y − a x i s .
a 2 x 2 + b 2 y 2 = 1 , w h e r e , a > b
The circles outside the triangle are tangent to the ellipse at each of the end points of the major axis, the equation of one such circle which lies entirely in the first and fourth quadrant is,
( x − ( a − r ) ) 2 + y 2 = r 2
Where r is the radius the of the circle. This equation gives of the feeling that the circle is tangent to the ellipse at one of the endpoint of the major axis; however, we check for the range of r (in terms of a and b ) for which the tangency is valid. After doing the necessary calculations, we obtain that the circle is tangent to the ellipse at one of the endpoint of the major axis of the ellipse if and only if r = a b 2 . Another condition is that 2 r < a so that the circle does not crosses origin (mid-point of the ellipse) so that the both the maximum area circles do not intersect.
A point on the aforementioned circle is given as ( a a 2 − b 2 + a b 2 sin ( α ) , a b 2 cos ( α ) ) for some α ∈ [ 0 , 2 π ] (Here, I have by mistake parameterized the coordinates of the point a point on the circle differently from the convention, however, this would not affect the end result). A line tangent to the circle at that point will be,
( a a 2 − b 2 + a b 2 sin ( α ) − a a 2 − b 2 ) ( x − a a 2 − b 2 ) + a b 2 cos ( α ) y = ( a b 2 ) 2 ⟹ a b 2 sin ( α ) ( x − a a 2 − b 2 ) + a b 2 cos ( α ) y = a 2 b 4
This line passes through the point ( 0 , b ) due to symmetry of the problem. Then,
a b 2 sin ( α ) ( 0 − a a 2 − b 2 ) + a b 2 cos ( α ) b = a 2 b 4
Hence, we obtain the following condition on α .
− a a 2 − b 2 sin ( α ) + b cos ( α ) = a b 2
Now, we will solve for the second point of intersection of the tangent line and ellipse ( X , Y ) . Substituting from the equation of line to the equation of ellipse and after much simplification we obtain,
( a 2 1 + b 2 tan 2 ( α ) ) X 2 − b 2 2 tan 2 ( α ) ( a a 2 − b 2 + a sin ( α b 2 ) X + b 2 tan 2 ( α ) ( a a 2 − b 2 + a sin ( α ) b 2 ) 2 − 1 = 0
A X 2 + B X + C = 0
Solving this equation would give us two values of X ; however, we realize that since we have already obtained α such that one of the intersection points is ( 0 , b ) , C must be zero.
When C = 0 ,
X = 0 , ( t r i v i a l ) , a n d , X = − B / A
Consequently we can obtain the Y coordinate for the non-trivial case.
Y = a cos ( α ) b 2 − tan ( α ) ( − A B − a a 2 − b 2 )
Now we can easily obtain the inradius of the triangle ( r i n ).
r i n = ( ∣ Y ∣ + b ) 2 ∣ X ∣ ∣ X ∣ 2 + ( ∣ Y ∣ + b ) 2
Notice that r i n and r , both, are functions of a and b only. The choice of a and b is inconsequential to our final result so we just assume a = 1 and choose c = a b , s u c h t h a t , 0 < c < 1 (the choice of a will only scale up or down the problem). Now we have obtained r i n and r as a function of c .
Now we'll solve for the value of c for which r i n = r where 0 < c < 1 / 2 . I used MATLAB for this purpose. Using the function f z e r o we obtain c = 0 . 5 7 6 1 2 7 1 1 0 5 1 6 1 0 0 . Now, we can obtain the corresponding θ from α .
θ = α − π = 4 . 2 3 8 9 6 7 9 7 5 2 1 0 1 4 9 − π = 1 . 0 9 7 3 7 5 . . .
Hence, ⌊ θ × 1 E + 6 ⌋ = 1 0 9 7 3 7 5 .
Here is the graph for variation of r i n and r with c .